
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式.
(3)直接写出y1>y2时x的取值范围.
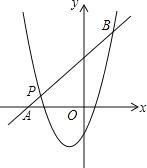
【答案】(1)m=2,n=2,(2)y=x+4;(3)x<-3或x>2
【解析】(1)∵对称轴是经过(1,0)且平行于y轴的直线,
∴![]() ,
,
∴m=2,
∵二次函数y=x2+mx+n的图象经过点P(3,1),
∴93m+n=1,得出n=3m8.
∴n=3m8=2;
(2)∵m=2,n=2,
∴二次函数关系式为y=x2+2x2,
过P作PC⊥x轴于C,BD⊥x轴于D,则PC∥BD,
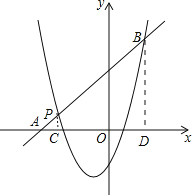
∴![]() ,
,
∵P (3,1),
∴PC=1,
∵PA:PB=1:5,
∴![]() ,
,
∴BD=6,
∴B的纵坐标为6,
代入二次函数为y=x2+2x2得,6=x2+2x2,
解得![]() =2,
=2,![]() =4(舍去),
=4(舍去),
∴B(2,6),
一次函数y2=kx+b经过了点B(2,6)、P(-3,1)则
![]()
解得![]()
∴一次函数的表达式为y=x+4
(3)x<-3或x>2


科目:初中数学 来源: 题型:
【题目】我们知道a+b=0时,a3+b3=0也成立,若将a看成a3的立方根,b看成b3的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数.
(1)试举一个例子来判断上述猜测结论是否成立;
(2)若![]() 与
与![]() 互为相反数,求
互为相反数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校期末表彰优秀,准备一次性购买若干钢笔和笔记本(每支钢笔的价格相同,每本笔记本的价格相同)作为奖品,若购买2支钢笔和3本笔记本共需62元,购买5支钢笔和1本笔记本共需90元.
(1)求购买一支钢笔和一本笔记本各需多少元?
(2)若学校共需要购买钢笔和笔记本共80件,而且要求购买的总费用不超过1100元,则最多可以购买多少支钢笔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果2x3yn+(m-2)x是关于x、y的五次二项式,则m、n的值为( )
A.m=3,n=2
B.m≠2,n=2
C.m为任意数,n=2
D.m≠2,n=3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com