
本题为选项做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.
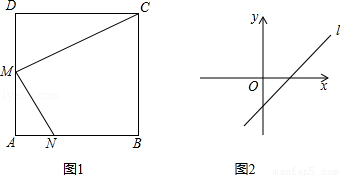
甲:直线l:y=(m﹣3)x+n﹣2(m,n为常数)的图象如图1所示,化简:|m﹣n|﹣ ;
;
乙:已知:如图2,在边长为a的正方形ABCD中,M是边AD的中点,能否在边AB上找到点N(不含A、B),使得△MAN相似?若能,请给出证明;若不能,请说明理由.
【解析】
试题分析:(1)根据函数图象确定m、n的取值范围,再化简.
(2)作NM⊥CM即可,可根据相似三角形的判定来证明.
解(甲题)由图象可知:m﹣3>0且n﹣2<0,(2分)
∴m>3且n<2.(4分)
|m﹣n|﹣ ﹣|m﹣1|=m﹣n﹣(2﹣n)﹣(m﹣1)(7分)
﹣|m﹣1|=m﹣n﹣(2﹣n)﹣(m﹣1)(7分)
=﹣1(9分)
(乙题)猜想:当AN=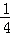 a时,△CDM∽△MAN.(2分)
a时,△CDM∽△MAN.(2分)
证明:在△CDM和△MAN中,
∵∠CDM=∠MAN=90°,
M是AD的中点,且四边形ABCD为正方形,(3分)
∴AM=DM= a,(4分)
a,(4分)
∴ ,(6分)
,(6分)
∴ (7分)
(7分)
∴△CDM∽△MAN.(9分)
考点:相似三角形的判定;一次函数图象与系数的关系.
点评:甲题根据一次函数与系数的关系确定m、n的取值范围,然后化简.乙题考查相似三角形的判定.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案科目:初中数学 来源: 题型:
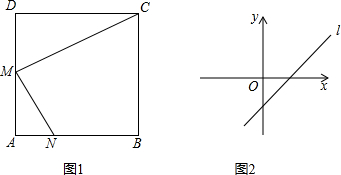
| n24n+4 |
查看答案和解析>>
科目:初中数学 来源:2013年初中数学单元提优测试卷-相似的判定(带解析) 题型:解答题
本题为选项做题,从甲、乙两题中选做一题即可,如果两题都做,只以甲题计分.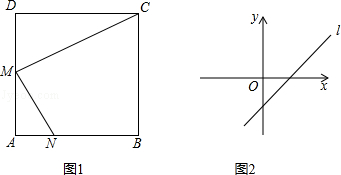
甲:直线l:y=(m﹣3)x+n﹣2(m,n为常数)的图象如图1所示,化简:|m﹣n|﹣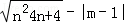 ;
;
乙:已知:如图2,在边长为a的正方形ABCD中,M是边AD的中点,能否在边AB上找到点N(不含A、B),使得△MAN相似?若能,请给出证明;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源:第27章《相似》中考题集(28):27.2 相似三角形(解析版) 题型:解答题
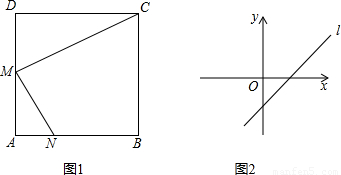
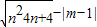 ;
;查看答案和解析>>
科目:初中数学 来源:第3章《图形的相似》中考题集(19):3.3 相似三角形的性质和判定(解析版) 题型:解答题
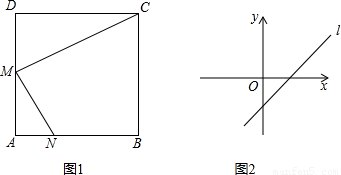
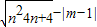 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com