
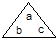 ”表示3abc,“方框
”表示3abc,“方框  表示(xm+yn).试计算:
表示(xm+yn).试计算: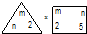
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
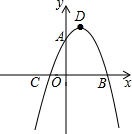 (2013•丹江口市模拟)如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B、C两点(B在C右边),顶点为D.
(2013•丹江口市模拟)如图,抛物线y=ax2-2ax-3a交y轴于A点,交x轴于B、C两点(B在C右边),顶点为D.查看答案和解析>>
科目:初中数学 来源:山东省模拟题 题型:解答题
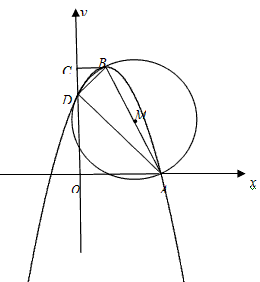
查看答案和解析>>
科目:初中数学 来源: 题型:
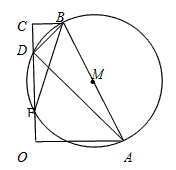
已知:直角梯形OABC中,BC∥OA,∠AOC=90°,以AB为直径的圆M
交OC于D、E,连结AD、BD、BE。
(1)在不添加其他字母和线的前提下,直接写出图1中的两对相似三角形。
_____________________,______________________
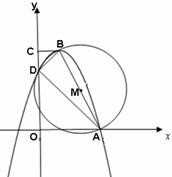
(2)直角梯形OABC中,以O为坐标原点,A在x轴正半轴上建立直角坐标系(如图2),
若抛物线y=ax2-2ax-3a(a<0)经过点A、B、D,且B为抛物线的顶点。
①写出顶点B的坐标(用a的代数式表示)___________。
②求抛物线的解析式。
③在x轴下方的抛物线上是否存在这样的点P:过点P做PN⊥x轴于N,
使得⊿PAN与⊿OAD相似?若存在,求出点P的坐标;若不存在,说明理由。
 | |||
 | |||
图1 图2
查看答案和解析>>
科目:初中数学 来源:第27章《二次函数》常考题集(26):27.3 实践与探索(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com