
如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),…直线ln⊥x轴于点(n,0).函数y=x的图象与直线l1,l2,l3…ln分别交于点A1,A2,A3,…An;函数y=2x的图象与直线l1,l2,l3…ln分别交于点B1,B2,B3…Bn,如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3…四边形An﹣1AnBnBn﹣1的面积记作Sn,那么S2014= _________ .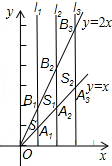
2013.5.
解析试题分析:根据直线解析式求出An-1Bn-1,AnBn的值,再根据直线ln-1与直线ln互相平行并判断出四边形An-1AnBn Bn-1是梯形,然后根据梯形的面积公式求出Sn的表达式,然后把n=2014代入表达式进行计算即可得解.
试题解析:根据题意,An-1Bn-1=2(n-1)-(n-1)=2n-2-n+1=n-1,
AnBn=2n-n=n,
∵直线ln-1⊥x轴于点(n-1,0),直线ln⊥x轴于点(n,0),
∴An-1Bn-1∥AnBn,且ln-1与ln间的距离为1,
∴四边形An-1AnBn Bn-1是梯形,
Sn= (n-1+n)×1=
(n-1+n)×1= (2n-1),
(2n-1),
当n=2014时,S2014= (2×2014-1)=2013.5.
(2×2014-1)=2013.5.
考点:一次函数图象上点的坐标特征.


科目:初中数学 来源:新人教版(2012) 七年级上 题型:
| |||||||||||||||
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
某仓库调拨一批物资,调进物资共用8小时,调进物资4小时后同时开始调出物资(调进与调出的速度保持不变).该仓库库存物资m(吨)与时间t(小时)之间的函数关系如图所示.则这批物资从开始调进到全部调出所需要的时间是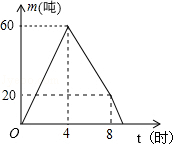
| A.8.4小时&nbs, | B.8.6小时&nbs, | C.8.8小时&nbs, | D.9小时&nbs, |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
在全民健身环城越野赛中,甲乙两选手的行程y(千米)随时间x(时)变化的图象(全程)如图所示。有下列说法:①起跑后1小时内,甲在乙的前面;②第1小时两人跑了10千米;③甲比乙先到达终点;④两人都跑了20千米。其中正确的说法有____________。(填入正确说法的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
在平面直角坐标系xOy中,一次函数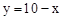 的图象与函数
的图象与函数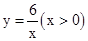 的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .
的图象相交于点A,B.设点A的坐标为(x1,y1),那么长为x1,宽为y1的矩形的面积为 ,周长为 .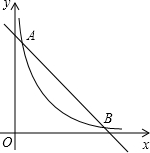
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,在直角坐标系中,正方形A1B1C1O、A2B2C2C1、A3B3C3C2、…AnBnCnCn﹣1的顶点A1、A2、A3、…、An均在直线y=kx+b上,顶点C1、C2、C3、…、Cn在x轴上,若点B1的坐标为(1,1),点B2的坐标为(3,2),那么点B4的坐标为 .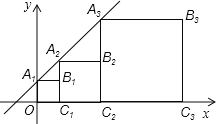
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,一次函数y1=k1x+b(k1≠0)的图象与反比例函数y2=k2x+b(k2≠0)的图象交于A,B两点,观察图象,当y1>y2时,x的取值范围是 .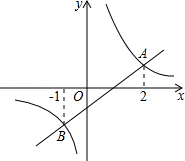
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间(单位:s)的函数如图②所示,则点P从开始移动到停止移动一共用了 秒(结果保留根号).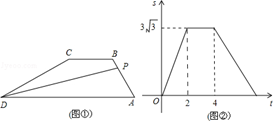
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com