分析:(1)由已知的一元二次方程,找出相应的a,b及c的值,根据阅读材料中的根与系数的关系式即可得出结果;
(2)同理找出已知方程的a,b及c的值,求出两根之和与两根之积,然后把所求的式子通分后,利用同分母分式相加的法则计算后,把得出的两根之和与两根之积的值代入即可求出值;
(3)同理找出已知方程的a,b及c的值,求出两根之和与两根之积,然后把所求的式子通分后,利用同分母分式相加的法则计算后,分子配方把平方和形式变为和的平方形式得到关于两根之和与两根之积的式子,把得出的两根之和与两根之积的值代入即可求出值.
解答:解:(1)∵a=1,b=4,c=-3,
∴x
1+x
2=-
=-4,x
1•x
2=
=-3;(2分)
(2)∵a=1,b=6,c=3,
∴x
1+x
2=-6,x
1•x
2=3,(3分)
∴
+===-2;(5分)
(3)∵a=1,b=-6,c=-5,
∴x
1+x
2=6,x
1•x
2=-5,(6分)
∴
+====-.(8分)
故答案为:-4;-3
点评:此题属于阅读理解型题,此类题取材广泛,题目灵活性大,要求学生通过阅读,理解材料中的内容、方法和思想,在此基础上按要求做出解答,既考查了学生的基础情况与自学能力,又考查了学生分析问题,利用规律解决问题的能力,此类题是近几年中考命题的热点之一,复习时应足够重视.本题主要考查了学生的阅读理解能力,以及代数式的变形能力.把所求的式子合理变形为只含有两根之和与两根之积的形式是解本题的关键.



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 20、阅读材料,解答问题.
20、阅读材料,解答问题.
 ,x1•x2=
,x1•x2= .
. +
+ 的值.
的值. ,x1•x2=
,x1•x2=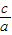 .
. +
+ 的值.
的值.