练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，∠BAC=90°，AB=AC，点D为边AC的中点，DE⊥BC于点E，连接BD，则tan∠DBC的值为（ ）

    A． B．﹣1 C．2﹣D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年江苏南京鼓楼区九年级上期中数学试卷（解析版） 题型：解答题

    我们知道，各类方程的解法虽然不尽相同，但是它们的基本思想都是“转化”，即把未知转化为已知．用“转化”的数学思想，我们还可以解一些新方程．

    认识新方程：

    像=x这样，根号下含有未知数的方程叫做无理方程，可以通过方程两边平方把它转化为2x+3=x2，解得x1=3，x2=﹣1．但由于两边平方，可能产生增根，所以需要检验，经检验，x2=﹣1是原方程的增根，舍去，所以原方程的解是x=3．

    运用以上经验，解下列方程：

    （1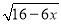）=x；

    （2）x+2=6．

    查看答案和解析>>

    科目：初中数学 来源：2017届吉林长春名校调研九年级上期中（市命题）数学试卷（解析版） 题型：选择题

    如图，AB∥CD∥EF，AF与BE相交于点G，且AG=2，GD=1，DF=5，那么的值等于（ ）

    A． B． C． D．

    查看答案和解析>>

    科目：初中数学 来源：2016届天津河西区中考模拟数学试卷（五）（解析版） 题型：填空题

    如图，直线l1、l2、…l6是一组等距的平行线，过直线l1上的点A作两条射线，分别与直线l3、l6相交于点B、E、C、F．若BC=2，则EF的长是 5 ．

    查看答案和解析>>

    科目：初中数学 来源：2016届天津河西区中考模拟数学试卷（五）（解析版） 题型：选择题

    如图，点A，B，C在一条直线上，△ABD，△BCE均为等边三角形，连接AE和CD，AE分别交CD，BD于点M，P，CD交BE于点Q，连接PQ，BM，下面结论：

    ①△ABE≌△DBC；②∠DMA=60°；③△BPQ为等边三角形；④MB平分∠AMC，

    其中结论正确的有（ ）

    A．1个 B．2个 C．3个 D．4个

    查看答案和解析>>

    科目：初中数学 来源：2016届陕西中考最后一模数学试卷（解析版） 题型：解答题

    如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点左侧，B点的坐标为（4，0），与y轴交于C（0，﹣4）点，点P是直线BC下方的抛物线上一动点．

    （1）求这个二次函数的表达式．

    （2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

    （3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．

    查看答案和解析>>

    科目：初中数学 来源：2016届陕西中考最后一模数学试卷（解析版） 题型：解答题

    用尺规作图从△ABC（CB＜CA）中裁出一个以AB为底边的等腰△ABD，并使得△ABD的面积尽可能大（保留作图痕迹，不要求写作法、证明）

    查看答案和解析>>

    科目：初中数学 来源：2016届内蒙古包头市青山区中考二模数学试卷（解析版） 题型：解答题

    已知直线y=kx+1经过点M（d，﹣2）和点N（1，2），交y轴于点H，交x轴于点F．

    （1）求d的值；

    （2）将直线MN绕点M顺时针旋转45°得到直线ME，点Q（3，e）在直线ME上，①证明ME∥x轴；②试求过M、N、Q三点的抛物线的解析式；

    （3）在（2）的条件下，连接NQ，作△NMQ的高NB，点A为MN上的一个动点，若BA将△NMQ的面积分为1：2两部分，且射线BA交过M、N、Q三点的抛物线于点C，试求点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2016届吉林长春二道区中考模拟数学试卷（5月份）（解析版） 题型：填空题

    比较大小： 2 （填“＜“，“=“或“＞“）．

    查看答案和解析>>

    同步练习册答案