Question

1．小玲要求△ABC最长边上的高，测得AB=8cm，AC=6cm，BC=10cm，则最长边上的高为4.8cm．

Answer 1

分析 先根据勾股定理的逆定理判断出三角形是直角三角形，然后根据面积法求解．

解答 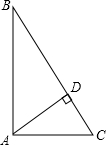解：∵AB²+AC²=6²+8²=100，BC²=10²=100，
∴三角形是直角三角形．
根据面积法求解：
S_△ABC=$\frac{1}{2}$AB•AC=$\frac{1}{2}$BC•AD（AD为斜边BC上的高），
即AD=$\frac{AB•AC}{BC}$=$\frac{8×6}{10}$=4.8（cm）．
故答案为：4.8．

点评 此题主要考查了勾股定理的逆定理以及三角形面积求法，解答此题要用到勾股定理的逆定理：已知三角形ABC的三边满足a²+b²=c²，则三角形ABC是直角三角形．以及三角形的面积公式求得斜边上的高．