
我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数 的图象与x轴交点的坐标为(
的图象与x轴交点的坐标为( ,0),所以该函数的零点是
,0),所以该函数的零点是 .
.
(1)函数 的零点是 ;
的零点是 ;
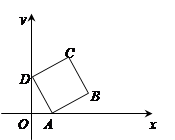
(2)如图,将边长为1的正方形ABCD放置在平面直角坐标系xOy中,且顶点A在x轴上.若正方形ABCD沿 轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在
轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在 轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与
轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与 轴所围区域的面积为 .
轴所围区域的面积为 .
(1)-5,0 (2)
解析试题分析:(1)函数 与x轴交点坐标(-5,0)。则零点为--5.
与x轴交点坐标(-5,0)。则零点为--5.
(2)解:依题意知,
则从A落在x轴上的时候开始计算,到下一次A点落在x轴上,这个过程中四个顶点依次落在了x轴上,而每两个顶点间距离为正方形的边长1,因此该函数的周期为4.下面考察P点的运动轨迹,不妨考察正方形向右滚动,D点从x轴上开始运动的时候,首先是围绕A点运动 个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BD为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如上,中间部分面积可看为
个圆,该圆半径为1,然后以B点为中心,滚动到C点落地,其间是以BD为半径,旋转90°,然后以C为圆心,再旋转90°,这时候以CP为半径,因此最终构成图象如上,中间部分面积可看为 半径为1的圆加上一个正方形面积:
半径为1的圆加上一个正方形面积:
故其与x轴所围成的图形面积为S=
考点:探究规律题
点评:本题难度中等。主要考查学生对几何图形面积综合探究规律掌握。为中考常见题型,要求学生培养数形结合思想,运用到考试中去。


科目:初中数学 来源: 题型:
 (2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-
(2013•丰台区一模)我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:2013年北京市丰台区中考一模考试数学试卷(解析版) 题型:填空题
我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数 的图象与x轴交点的坐标为(
的图象与x轴交点的坐标为( ,0),所以该函数的零点是
,0),所以该函数的零点是 .
.

(1)函数 的零点是 ;
的零点是 ;
(2)如图,将边长为1的正方形ABCD放置在平面直角坐标系xOy中,且顶点A在x轴上.若正方形ABCD沿 轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在
轴正方向滚动,即先以顶点A 为中心顺时针旋转,当顶点B落在 轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与
轴上时,再以顶点B为中心顺时针旋转,如此继续.顶点D的轨迹是一函数的图象,则该函数在其两个相邻零点间的图象与 轴所围区域的面积为 .
轴所围区域的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(-
我们把函数图象与x轴交点的横坐标称为这个函数的零点.如函数y=2x+1的图象与x轴交点的坐标为(- ,0),所以该函数的零点是-
,0),所以该函数的零点是- .
.查看答案和解析>>
科目:初中数学 来源:2013年北京市丰台区中考数学一模试卷(解析版) 题型:填空题
 ,0),所以该函数的零点是-
,0),所以该函数的零点是- .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com