
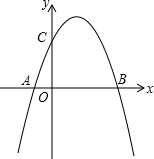
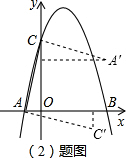
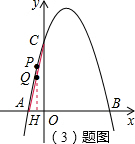
 如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.
如图,抛物线y=ax2-3ax+b与x轴交于A和B(4,0),与y轴交于C点,并且OB=OC,点P为抛物线上一点.
|
|
|
|
| 1 |
| 4 |
| 1 |
| 4 |
|
|
|
| 17 |
| 4 |
| 21 |
| 16 |
|
|
| 1 |
| 4 |
|
|
|
| 13 |
| 4 |
| 51 |
| 16 |
| 17 |
| 4 |
| 21 |
| 16 |
| 13 |
| 4 |
| 51 |
| 16 |
|
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
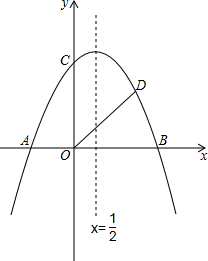 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
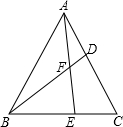 已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )
已知△ABC是等边三角形,点D、E分别在AC、BC边上,且AD=CE,AE与BD交于点F,则∠AFD的度数为( )| A、60° | B、45° |
| C、75° | D、70° |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
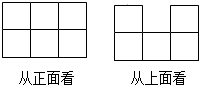 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:
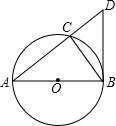 如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.
如图:⊙O是△ABC的外接圆,圆心O在AB上,过点B作⊙O的切线交AC的延长线于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com