
给出以下命题:(1)55,98,62,61,57这组数据的中位数是61;(2)若![]() ,则
,则![]() 必有意义;(3)过弦的中点的直径一定垂直于这条弦;(4)圆是轴对称图形,也是中心对称图形,其中所有正确命题的代号是(
)
必有意义;(3)过弦的中点的直径一定垂直于这条弦;(4)圆是轴对称图形,也是中心对称图形,其中所有正确命题的代号是(
)
A
.(1)、(2)、(4) B.(1)、(3)、(4)C
.(2)、(3) D.(1)、(4) 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
| ||
| a+1 |
| A、(1),(2),(4) |
| B、(1),(3),(4) |
| C、(2),(3) |
| D、(1),(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(福建漳州卷)数学(解析版) 题型:解答题
(1)问题探究
数学课上,李老师给出以下命题,要求加以证明.
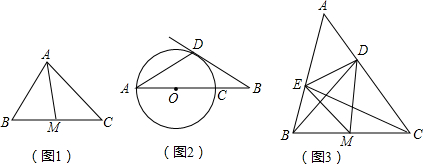
如图1,在△ABC中,M为BC的中点,且MA= BC,求证∠BAC=90°.
BC,求证∠BAC=90°.
同学们经过思考、讨论、交流,得到以下证明思路:
思路一 直接利用等腰三角形性质和三角形内角和定理…
思路二 延长AM到D使DM=MA,连接DB,DC,利用矩形的知识…
思路三 以BC为直径作圆,利用圆的知识…
思路四…
请选择一种方法写出完整的证明过程;
(2)结论应用
李老师要求同学们很好地理解(1)中命题的条件和结论,并直接运用(1)命题的结论完成以下两道题:
①如图2,线段AB经过圆心O,交⊙O于点A,C,点D在⊙O上,且∠DAB=30°,OA=a,OB=2a,求证:直线BD是⊙O的切线;
②如图3,△ABC中,M为BC的中点,BD⊥AC于D,E在AB边上,且EM=DM,连接DE,CE,如果∠A=60°,请求出△ADE与△ABC面积的比值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com