
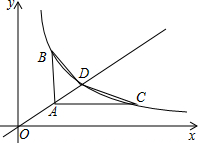
 直线y=$\frac{2}{3}x$与双曲线y=$\frac{6}{x}$(x>0)相交于点D.
直线y=$\frac{2}{3}x$与双曲线y=$\frac{6}{x}$(x>0)相交于点D.分析 (1)解方程组即可得到结果;
(2)设A(m,$\frac{2}{3}$m),则B(m,$\frac{6}{m}$),C($\frac{9}{m}$,$\frac{2}{3}$m),得到AB=|$\frac{6}{m}$-$\frac{2}{3}$m|,AC=|$\frac{9}{m}$-m|,①当0<m<3时,②当m>3时,求得AB,AC,于是得到结论;
(3)根据三角形的面积公式即可得到结论.
解答 解:(1)解方程组$\left\{\begin{array}{l}{y=\frac{2}{3}x}\\{y=\frac{6}{x}}\end{array}\right.$得:$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$(舍去负值),
∴点D的坐标为(3,2);
(2)设A(m,$\frac{2}{3}$m),则B(m,$\frac{6}{m}$),C($\frac{9}{m}$,$\frac{2}{3}$m),
∴AB=|$\frac{6}{m}$-$\frac{2}{3}$m|,AC=|$\frac{9}{m}$-m|,
①当0<m<3时,AB-AC=$\frac{6}{m}$-$\frac{2}{3}$m-$\frac{9}{m}$+m=$\frac{m}{3}$-$\frac{3}{m}$=$\frac{{m}^{2}-9}{3m}$<0,∴AB<AC;
②当m>3时,AB=$\frac{2}{3}$m-$\frac{6}{m}$,AC=m-$\frac{9}{m}$,
∴AB-AC=$\frac{2}{3}$m-$\frac{6}{m}$-m+$\frac{9}{m}$=$\frac{{m}^{2}+3}{3m}$>0,
∴AB>AC;
(3)$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{AB•(3-m)}{AC•(2-\frac{2}{3}m)}$=$\frac{(\frac{6}{m}-\frac{2}{3}m)(3-m)}{(\frac{9}{m}-m)(2-\frac{2}{3}m)}$=1.
点评 本题考查了反比例函数与一次函数的交点问题,比较线段的大小,三角形面积的计算,正确的理解题意是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 销售单价x元/公斤 | … | 30 | 35 | 40 | 45 | … |
| 销售量y公斤 | … | 500 | 450 | 400 | 350 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 77.3 | B. | 91 | C. | 81 | D. | 78 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}$ | B. | $\sqrt{12}$ | C. | $\sqrt{7}$ | D. | $\sqrt{\frac{1}{3}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
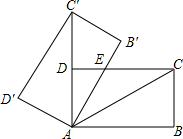 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置.此时AC′的中点恰好与点D重合,AB′交CD于点E,若AB=3,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置.此时AC′的中点恰好与点D重合,AB′交CD于点E,若AB=3,则△AEC的面积为( )| A. | 3 | B. | $\frac{3}{2}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com