
 在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.
在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.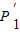 ,使△
,使△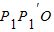 为等边三角形时,求OP1所在直线的解析式;
为等边三角形时,求OP1所在直线的解析式; ,且y2=
,且y2= 时,求梯形P1
时,求梯形P1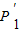
 P2的面积.
P2的面积.
 xy=2,根据对称的性质得到S△P′PO=2S△OPH=4;
xy=2,根据对称的性质得到S△P′PO=2S△OPH=4; 为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A=
为等边三角形,得OP1与y轴的夹角为30°,则∠AOP1=60°,利用含30度的直角三角形三边的关系得到P1A=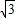 OA,这样可设P1的坐标为(x1,
OA,这样可设P1的坐标为(x1,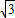 x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k=
x1),直线OP1的解析式为y=kx,然后把P1的坐标代入可解得k=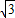 ,从而确定OP1所在直线的解析式;
,从而确定OP1所在直线的解析式;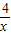 上,且y2=
上,且y2=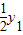 ,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2=
,可得到x1•y1=4,x2•y2=4,x2=2x1,则P1C=y1-y2= y1,利用梯形的面积公式得到梯形P1
y1,利用梯形的面积公式得到梯形P1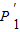
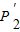 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C=
(P1P1′+P2P2′)•P1C= (2x1+2x2)(y1-y2)=
(2x1+2x2)(y1-y2)= •6x1•
•6x1• y1,把x1•y1=4代入计算即可.
y1,把x1•y1=4代入计算即可.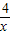 ,
, xy=2,
xy=2,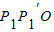 为等边三角形,
为等边三角形,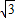 OA,
OA,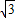 x1),直线OP1的解析式为y=kx,
x1),直线OP1的解析式为y=kx,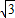 ,
,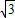 x;
x;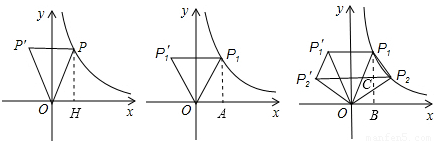
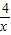 上,且y2=
上,且y2=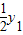 ,
, y1,
y1,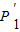
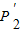 P2的面积=
P2的面积= (P1P1′+P2P2′)•P1C
(P1P1′+P2P2′)•P1C (2x1+2x2)(y1-y2)
(2x1+2x2)(y1-y2) •6x1•
•6x1• y1
y1 •x1•y1
•x1•y1 ×4
×4

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
| 3 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:
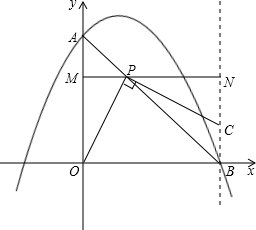 行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.
行于x轴,交y轴于点M,交过点B垂直于x轴的直线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| x |
| P | ′ 1 |
| P | ′ 2 |
| 1 |
| 2 |
| P | ′ 1 |
| P | ′ 2 |
查看答案和解析>>
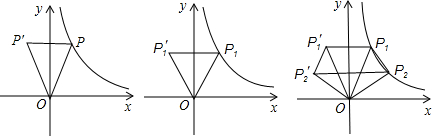
科目:初中数学 来源: 题型:解答题
 在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.
在第一象限的图象上的任一点,点P关于y轴的对称点为P′,连接P′P、P′O、OP.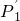 ,使△
,使△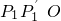 为等边三角形时,求OP1所在直线的解析式;
为等边三角形时,求OP1所在直线的解析式; ,且y2=
,且y2=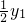 时,求梯形P1
时,求梯形P1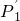
 P2的面积.
P2的面积.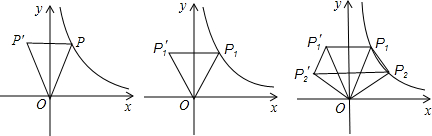
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com