
【题目】如图,已知△ABC中,BD平分∠ABC,点M是BD上一点,过M点作EF∥BC,分别交AB、AC于E、F,作MN∥AB交BC于N.
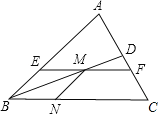
(1)试判断四边形BEMN是什么特殊四边形?并证明你的结论.
(2)连接EN,将△ABC再添加一个什么条件时,四边形EFCN是平行四边形?
【答案】(1)平行四边形BEMN是菱形;(2)BA=BC(条件答案不唯一).
【解析】
试题分析:因为四边形BEMN的对边都互相平行很容易得到是平行四边形,又因为BD平分∠ABC,所以很容易证得△BEM是等腰三角形所以BE=EM,所以四边形BEMN是菱形;添一个条件:BA=BC即可.
解:(1)四边形BEMN是菱形,
∵EF∥BC,MN∥AB,
∴四边形BEMN是平行四边形,
∵EF∥BC,
∴∠EMB=∠MBN,
又∵∠EBM=∠MBN,
∴∠EMB=∠EBM,
∴EB=EM,
∴平行四边形BEMN是菱形;
(2)条件:BA=BC(条件答案不唯一).
∵BA=BC,BD平分∠ABC,
∴BD⊥AC,
∵四边形BEMN是菱形,
∴BD⊥EN,
∴AC∥EN,
又∵EF∥CN,
∴四边形EFCN是平行四边形.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】下列各命题的逆命题成立的是( )
A. 对顶角相等B. 如果a=b,那么|a|=|b|
C. 全等三角形的对应角相等D. 两直线平行,同位角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=﹣2x2向上平移1个单位,再向右平移1个单位,得到的抛物线是( )
A.y=﹣2(x+1)2+1
B.y=﹣2(x﹣1)2+1
C.y=﹣2(x﹣1)2﹣1
D.y=﹣2(x+1)2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车4S店销售某种型号的汽车,每辆进货价为15万元,该店经过一段时间的市场调研发现:当销售价为25万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出1辆.该4S店要想平均每周的销售利润为90万元,并且使成本尽可能的低,则每辆汽车的定价应为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
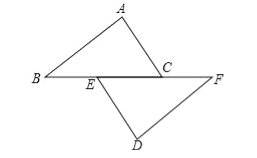
【题目】如图,已知点B,E,C,F在一条直线上,AB=DF,AC=DE,∠A=∠D.
(1)求证:AC∥DE;
(2)若BF=13,EC=5,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com