
 的值;
的值; MN×OP=
MN×OP= ×2c×b2=b2c,
×2c×b2=b2c, ×ON×OP=
×ON×OP= |a-c|×b2,
|a-c|×b2, |a-c|×b2,
|a-c|×b2, =
=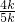 =
= ;
;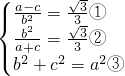 ,
,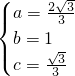 .
. 的值易求;
的值易求; ,得出
,得出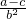 =
= ①,同理,在直角△OPM中,由tan∠NMP=
①,同理,在直角△OPM中,由tan∠NMP= ,得出
,得出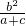 =
= ②,又由(1)可知b2+c2=a2③,①②③联立,得到方程组,解此方程组即可求解.
②,又由(1)可知b2+c2=a2③,①②③联立,得到方程组,解此方程组即可求解.

科目:初中数学 来源: 题型:
 (2012•鼓楼区二模)已知反比例函数y1=
(2012•鼓楼区二模)已知反比例函数y1=| k |
| x |
| k |
| x |
| k |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:课堂三级讲练数学九年级(上) 题型:013
已知a、b、c是△ABC的三条边的长,那么方程cx2-(a+b)x+![]() =0的根的情况是
=0的根的情况是
[ ]
A.没有实根
B.有两个不相等的正实数根
C.有两个不相等的负实数根
D.有两个异号实数根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com