
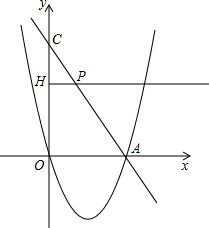
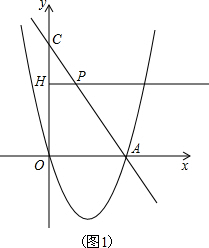
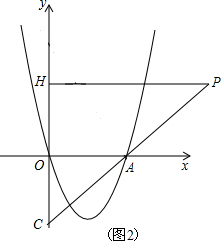
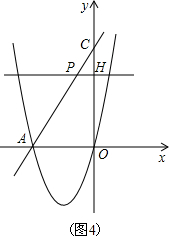
 如图,经过原点的抛物线y=x2-2mx与x轴的另一个交点为A.过点P(m+1,
如图,经过原点的抛物线y=x2-2mx与x轴的另一个交点为A.过点P(m+1,| 1 |
| 2 |
| 3 |
| 2 |
| HP |
| OA |
| CH |
| CO |
| 1 |
| 2 |
| 3 |
| 2 |
| m+1 |
| 2m |
| 1 |
| 1.5 |
| HP |
| OA |
| CH |
| CO |
| m+1 |
| 2m |
| 1 |
| 2.5 |

| HP |
| OA |
| CH |
| CO |
| m+1 |
| -2m |
| 1 |
| 2.5 |
| 5 |
| 9 |
| 1 |
| 2 |
| 1 |
| 7 |
| 5 |
| 14 |
| 5 |
| 14 |
| HP |
| OA |
| CH |
| CO |
| -m-1 |
| -2m |
| 1 |
| 2.5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 5 |
| 6 |
| 5 |
| 6 |
| 5 |
| 9 |
| 5 |
| 14 |
| 5 |
| 6 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
| 1 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3
(2013•湖州)如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为3| 2 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省江阴市顾山九年级上学期期末考试数学试卷(解析版) 题型:选择题
.如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为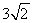 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
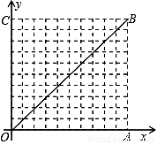
A.13?????? B.14? ???? C.15?????? D.16
查看答案和解析>>
科目:初中数学 来源:2013年浙江省湖州市中考数学试卷(解析版) 题型:选择题
 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.若抛物线经过图中的三个格点,则以这三个格点为顶点的三角形称为抛物线的“内接格点三角形”.以O为坐标原点建立如图所示的平面直角坐标系,若抛物线与网格对角线OB的两个交点之间的距离为 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是( )查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江苏南通卷)数学(解析版) 题型:解答题
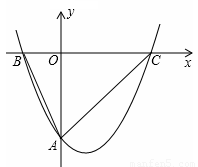
如图,经过点A(0,-4)的抛物线y=x2+bx+c与x轴相交于点B(-0,0)和C,O为坐标原点.
(1)求抛物线的解析式;
(2)将抛物线y=x2+bx+c向上平移个单位长度、再向左平移m(m>0)个单位长度,得到新抛物
线.若新抛物线的顶点P在△ABC内,求m的取值范围;
(3)设点M在y轴上,∠OMB+∠OAB=∠ACB,求AM的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com