

分析 首先根据共支付给旅行社旅游费用27000元,如果人均旅游费用1000元,可知人数超过25人,然后根据每人的旅游费用×人数=总费用,设该单位这次共有x名员工去大青山风景区旅游,可由对话框,超过25人的人数为(x-25)人,每人降低20元,共降低了20(x-25)元.实际每人收了[1000-20(x-25)]元,列出方程求解.
解答 解:设该单位这次共有x名员工去大青山风景区旅游.
因为1000×25=25000<27000,所以员工人数一定超过25人.
可得方程[1000-20(x-25)]x=27000,
整理得x2-75x+1350=0,
解得x1=45,x2=30.
当x1=45时,1000-20(x-25)=600<700,故舍去x1;
当x2=30时,1000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去大青山风景区旅游.
点评 本题主要考查一元二次方程的应用,此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,注意舍去不合题意的解.


科目:初中数学 来源: 题型:解答题
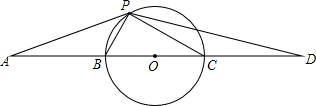 如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.
如图,点B,C是线段AD的三等分点,以BC为直径作⊙O,点P是圆上异于B,C的任意一点,连接PA,PB,PC,PD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
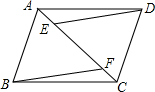 如图,已知四边形ABCD中,连接AC,点E、F在AC上,AE=CF,连接DE,BF,且DE$\underset{∥}{=}$BF,求证:四边形ABCD是平行四边形.
如图,已知四边形ABCD中,连接AC,点E、F在AC上,AE=CF,连接DE,BF,且DE$\underset{∥}{=}$BF,求证:四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
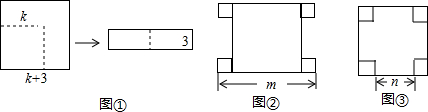
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
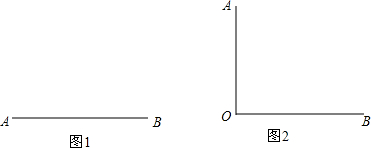
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2016-2017学年福建省泉州市泉港区2016-2017学年八年级3月教学质量检测数学试卷(解析版) 题型:单选题
点M(1,2)关于x轴对称点的坐标为( )
A. (-1,2) B. (-1,-2) C. (1,-2) D. (2,-1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com