
| ���۵���x/Ԫ | 4 | 5 | 6 | 7 | 8 |
| ��������t/�� | 120 | 100 | 80 | 60 | 40 |
���� ��1�����ݱ�����Է���t��x��һ�κ�����ϵ���Ӷ�������������ʽ���Ӷ����������������t�����۵���x֮��Ĺ�ϵ��
��2����������������ÿ�������P��Ԫ�������۵���x�ĺ�����ϵ��
��3��������ϵʵ�ʿ�֪���յĵܵܵĹ۵��Ǵ���ģ�Ȼ����ݣ�2���еĹ�ϵʽ���仯Ϊ����ʽ�����ɽ���⣮
��� �⣺��1������������t�����۵���x֮��Ĺ�ϵΪ��t=kx+b��
��$\left\{\begin{array}{l}{4k+b=120}\\{5k+b=100}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-20}\\{b=200}\end{array}\right.$��
��������t�����۵���x֮��Ĺ�ϵ��t=-20x+200��
��2��������ɵã�
P=x��-20x+200��-[3��-20x+200��+100]=-20x2+260x-700��
��ÿ�������P��Ԫ�������۵���x�ĺ�����ϵ�ǣ�P=-20x2+260x-700��
��3����ͬ�����յܵܵĹ۵㣬
��P=-20x2+260x-700=$-20��x-\frac{13}{2}��^{2}+145$��
�൱x=$\frac{13}{2}$ʱ��ȡ���������ʱ�������Ϊ145Ԫ��
��ÿ������������145Ԫ��
���� ���⿼����κ�����Ӧ�ã�����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ��������֪�����κ��������ʣ��Ὣ������ϵʽ��Ϊ����ʽ��


 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
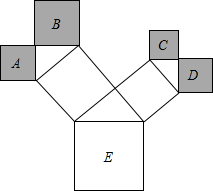 ��ͼ��һ�������Ĺ��������������е��ı��ζ��������Σ����е������ζ���ֱ�������Σ���������A��B��C��D������ֱ���4��6��3��4�������������E�������17��
��ͼ��һ�������Ĺ��������������е��ı��ζ��������Σ����е������ζ���ֱ�������Σ���������A��B��C��D������ֱ���4��6��3��4�������������E�������17���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{m}{n}$һ������$\frac{1}{2}$ | |
| B�� | $\frac{m}{n}$һ��������$\frac{1}{2}$ | |
| C�� | $\frac{m}{n}$һ������$\frac{1}{2}$ | |
| D�� | Ͷ���Ĵ����ܶ�ʱ��$\frac{m}{n}$�ȶ���$\frac{1}{2}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��7-x=13����x=13-7 | B�� | ��5x=4x+8����5x-4x=8 | ||
| C�� | ��$\frac{1}{2}$x=1����x=$\frac{1}{2}$ | D�� | ��7x+6=5x����7x-5x=6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
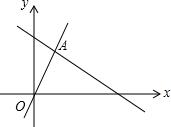 ��ͼ������y=2x��y=ax+4��ͼ���ཻ�ڵ�A��$\frac{3}{2}��3$������ʽ2x��ax+4�Ľ⼯Ϊx��$\frac{3}{2}$��
��ͼ������y=2x��y=ax+4��ͼ���ཻ�ڵ�A��$\frac{3}{2}��3$������ʽ2x��ax+4�Ľ⼯Ϊx��$\frac{3}{2}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com