
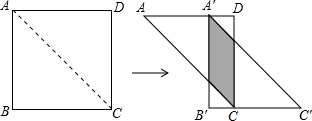
 解:设AC交A′B′于H,
解:设AC交A′B′于H,

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:
 某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:
某校为了了解九年级男生立定跳远的成绩,从该校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成下面的扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
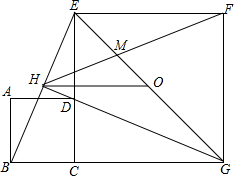 如图,正方形ABCD的边CD与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:
如图,正方形ABCD的边CD与正方形CGFE的边CE重合,O是EG的中点,∠EGC的平分线GH过点D,交BE于H,连接OH、FH、EG与FH交于M,对于下面四个结论:| ∥ |
. |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com