
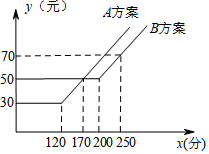
 如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )
如图,某电脑公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分钟)之间的关系,则以下说法错误的是( )| A. | 若通话时间少于120分,则A方案比B方案便宜20元 | |
| B. | 若通讯费用为60元,则B方案比A方案的通话时间多 | |
| C. | 若两种方案通讯费用相差10元,则通话时间是145分或185分 | |
| D. | 若通话时间超过200分,则B方案比A方案便宜12元 |
分析 当B方案为50元时,A方案如果是40元或者60元,才能使两种方案通讯费用相差10元,先求两种方案的函数解析式,再求对应的时间.
解答 解:A方案的函数解析式为:yA=$\left\{\begin{array}{l}{30(0<x≤120)}\\{\\;\frac{2}{5}\\;x-18(x>120)}\end{array}\right.$;
B方案的函数解析式为:yB=$\left\{\begin{array}{l}{50(0<x≤200)}\\{\\;\frac{2}{5}\\;x-30(x>200)}\end{array}\right.$;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故C错误;
观察函数图象可知A、B、D正确.
故选C
点评 本题需注意两种付费方式都是分段函数,难点是根据所给函数上的点得到两个函数的解析式,而后结合图象进行判断.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查春节联欢晚会的收视率 | |
| B. | 选出某校短跑最快的学生参加全区比赛 | |
| C. | 检测某批次火柴的质量 | |
| D. | 鞋厂检测生产的鞋底能承受的弯折次数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
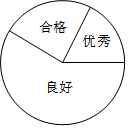 某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.
某校学生参加某项数学检测的成绩被分为优秀、良好、合格三个等级,其人数比为2:7:3,如图所示的扇形图表示上述分布情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).
已知△ABC的三个顶点的坐标分别是A(-2,3),点B(0,1),点C(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
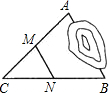 如图,A、B两点分布在水池的两边,一学生在AB外选取了一点C,连接AC和BC,并分别找出各自中点M、N,若测得MN=20m,则A、B两点的距离为( )
如图,A、B两点分布在水池的两边,一学生在AB外选取了一点C,连接AC和BC,并分别找出各自中点M、N,若测得MN=20m,则A、B两点的距离为( )| A. | 25 | B. | 30 | C. | 35 | D. | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
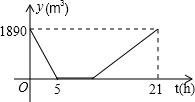 某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:
某游泳池内现存水1890(m3),已知该游泳池的排水速度是灌水速度的2倍.假设在换水时需要经历“排水--清洗--灌水”的过程,其中游泳池内剩余的水量y(m3)与换水时间t(h)之间的函数关系如图所示.根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com