解:(1)∵x
2=3,
∴x
1=x
2=

;
(2)∵(x-1)
2=9,
∴x-1=3或x-1=-3,
∴x
1=4,x
2=-2.
故答案为x
1=x
2=

;x
1=4,x
2=-2.
(3)∵8x
3=125,
∴2x=5,
∴x=

;
(4)∵x-2的平方根是±2,2x+y+7的立方根是3,
∴x-2=4,2x+y+7=27,解得x=6,y=8,
∴x
2+y
2=6
2+8
2=100,
∴求x
2+y
2的平方根为±10;
(5)∵2x-1≥0且1-2x≥0,
∴x=

,
∴y=1,
∴x
y=(

)
1=

.
分析:(1)、(2)先移项,然后利用直接开平方法解方程;
(3)移项得到8x
3=125,然后两边开立方即可得到x的值;
(4)根据平方根和立方根的定义得到x-2=4,2x+y+7=27,可解得x=6,y=8,再计算x
2+y
2,然后再根据平方根的定义求出x
2+y
2的平方根;
(5)根据二次根式有意义的条件得到2x-1≥0且1-2x≥0,解得x=

,易得y=1,然后代入x
y中计算即可.
点评:本题考查了实数的运算:先进行乘方或开方运算,再进行实数的乘除运算,然后进行实数的加减运算.也考查了平方根与立方根的定义.

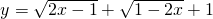 ,求xy的值.
,求xy的值. ;
; ;x1=4,x2=-2.
;x1=4,x2=-2. ;
; ,
, )1=
)1= .
. ,易得y=1,然后代入xy中计算即可.
,易得y=1,然后代入xy中计算即可.
