
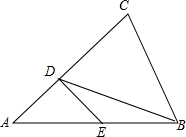
 如图,点D在AC上,点E在AB上,且AB=AC,BD=BC,AD=DE=BE.求∠A的度数.
如图,点D在AC上,点E在AB上,且AB=AC,BD=BC,AD=DE=BE.求∠A的度数. 分析 设∠A=x°,根据等边对等角和三角形的一个外角等于与它不相邻的两个内角的和表示出∠ABD,再表示出∠BDC,根据等边对等角可得∠C=∠BDC,∠C=∠ABC,然后利用三角形的内角和等于180°列方程求解即可.
解答 解:设∠A=x°,
∵AD=DE=BE,
∴∠ABD=∠BDE,∠A=∠AED,
由三角形的外角性质得,∠AED=∠ABD+∠BDE=2∠ABD,
∴∠ABD=$\frac{1}{2}$x°,
在△ABD中,∠BDC=∠A+∠ABD=x°+$\frac{1}{2}$x°=$\frac{3}{2}$x°,
∵BD=BC,
∴C=∠BDC,
∵AB=AC,
∴∠C=∠ABC,
∴∠ABC=∠C=∠BDC=$\frac{3}{2}$x°,
在△ABC中,由三角形内角和定理得,
x+$\frac{1}{2}$x+$\frac{3}{2}$x=180,
解得x=45,
所以,∠A=45°.
点评 本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,熟记性质与定理并最终列出方程是解题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
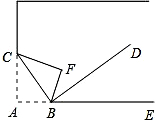 小东将书折过来,该角顶点A落在F处,BC为折痕,如图所示,若DB平分∠FBE,∠DBE比∠CBA大30°,设∠CBA和∠DBE分别为x°、y°,那么可求出这两个角的度数的方程组是$\left\{\begin{array}{l}{2x+2y=180}\\{y-x=30}\end{array}\right.$.
小东将书折过来,该角顶点A落在F处,BC为折痕,如图所示,若DB平分∠FBE,∠DBE比∠CBA大30°,设∠CBA和∠DBE分别为x°、y°,那么可求出这两个角的度数的方程组是$\left\{\begin{array}{l}{2x+2y=180}\\{y-x=30}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,A,B 两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出A,B间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长为30m,由此他就知道了A,B间的距离.请你写出小明的依据三角形的中位线等于第三边的一半,A,B间的距离是60m.
如图,A,B 两地被池塘隔开,在没有任何测量工具的情况下,小明通过下面的方法估测出A,B间的距离:先在AB外选一点C,然后步测出AC,BC的中点M,N,并测出MN的长为30m,由此他就知道了A,B间的距离.请你写出小明的依据三角形的中位线等于第三边的一半,A,B间的距离是60m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com