

 ;设BF=x2.根据S△AFQ+2S△BFC=S△ABC,解得x2=
;设BF=x2.根据S△AFQ+2S△BFC=S△ABC,解得x2= ,同理解得,x3=
,同理解得,x3= ,然后利用∴S△DEF=S△ABC-S△AEF-S△BFD-S△CDE,将所得数值代入即可.
,然后利用∴S△DEF=S△ABC-S△AEF-S△BFD-S△CDE,将所得数值代入即可.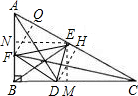 解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC.
解:过F点作FQ⊥AC,过E点⊥作NE⊥AB,EM⊥BC,过D点作DH⊥AC. x1(4-x1)+
x1(4-x1)+ x1(3-x1)=
x1(3-x1)= ×12,
×12, ;
; x2×1+2(
x2×1+2( x2×4)=
x2×4)= ×12,
×12, ,
, ;
; ,
, =
= ,
, AB•BC-
AB•BC- AF•NE-
AF•NE- BF•FD-
BF•FD- CD•EM
CD•EM (
( ×
× )-
)- (
( ×
× )-
)- (
( ×
× )
) .
. .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com