
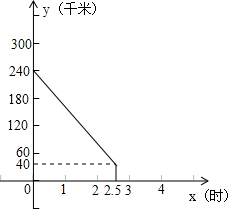
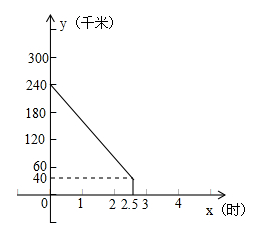
 南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.
南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.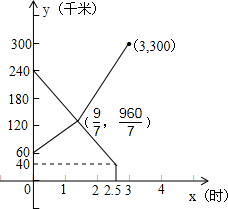
| 9 |
| 7 |
| 960 |
| 7 |
| 9 |
| 7 |
| 960 |
| 7 |
| 960 |
| 7 |
| 9 |
| 7 |


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
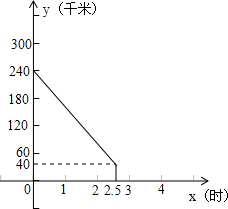 南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.
南京至上海的沪宁高速公路长约300千米.甲、两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速上正常行驶.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离y(千米)与行驶时间x(时)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
南京至上海的沪宁高速公路长约300千米.甲、乙两车同时分别从距南京240千米、60千米的入口行驶上沪宁高速公路.甲车驶往南京、乙车驶往上海.甲车在行驶过程中速度始终不变.甲车离南京(沪宁高速公路南京起点)的距离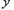 (千米)与行驶时间
(千米)与行驶时间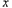 (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.
(1)求出甲车离南京的距离)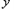 (千米)与行驶时间
(千米)与行驶时间 (时)之间的函数表达式;
(时)之间的函数表达式;
(2)乙车若以60千米/时的速度匀速行驶,1小时后两车相距多少千米?
(3)乙车按(2)中状态行驶与甲车相遇后,速度改为a千米/时,结果两车同时到达沪宁高速南京、上海起点,求乙车变化后的速度a;并在如图所示的直角坐标系中,画出乙车离南京的距离)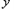 (千米)与行驶时间
(千米)与行驶时间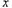 (时)之间的函数图像
(时)之间的函数图像
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com