
分析 (1)把等号左边的式子利用幂的乘方转化为以3为底数的幂,根据等式的左边=右边,即可求解.
(2)把等号左边的式子利用幂的乘方以及同底数的幂的乘法法则转化为以2为底数的幂,则对应的指数相等,即可求解;
(3)把等号左边的式子利用积的乘方的逆运用转化为以15为底数的幂,则对应的指数相等,即可求解.
解答 解:(1)27x=(33)x=33x=39,
∴3x=9,
解得:x=3.
(2)2÷8x•16x=2÷(23)x•(24)x=2÷23x•24x=21-3x+4x=25,
∴1-3x+4x=5,
解得:x=4.
(3)3x+2•5x+2=(3×5)x+2=15x+2=153x-8,
∴x+2=3x-8,
解得:x=5.
点评 本题考查了幂的乘方和积的乘方,解决本题的关键是熟记幂的乘方和积的乘方法则.


科目:初中数学 来源: 题型:选择题
| A. | “a不是负数”表示为a>0 | |
| B. | “m与4的差是非负数”表示为m-4≥0 | |
| C. | “x不大于3”表示为x≤3 | |
| D. | “代数式x2+3大于3x-7”表示为x2+3>3x-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
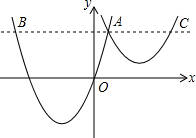 如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )
如图,抛物线y1=a(x+2)2-3与y2=$\frac{1}{2}$(x-3)2+1交于点A(1,3),过点A作x轴的平行线,分别交两条抛物线于点B,C.则以下结论:①无论x取何值,y2的值总是正数;②a=$\frac{2}{3}$;③当x=0时,y2-y1=6;④AB+AC=10;其中正确结论的个数是( )| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com