
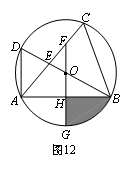
如图12,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,
交AB于H,交⊙O于G.
(1)求证:![]() ;
;
(2)若⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,
求阴影部分的面积.(结果保留根号)
 (1)∵BD是直径,∴∠DAB=90°.………………(1分)
(1)∵BD是直径,∴∠DAB=90°.………………(1分)
∵FG⊥AB,∴DA∥FO.
∴∠EOF=∠EDA,∠EFO=∠EAD.
∴△FOE∽△ADE.
∴![]() .即OF·DE=OE·AD. ……(3分)
.即OF·DE=OE·AD. ……(3分)
∵O是BD的中点,DA∥OH,
∴AD=2OH.……………………………………(4分)
∴OF·DE=OE·2OH.………………………………………………………(5分)
(2)∵⊙O的半径为12,且OE∶OF∶OD=2∶3∶6,
∴OE=4,ED=8,OF=6.…………………………………………………(6分)
代入(1)结论得AD=12. ∴OH=6.
在Rt△ABC中,OB=2OH,∴∠BOH=60°.
∴BH=BO·sin60°=12×![]() =6
=6![]() .………………………………………(8分)
.………………………………………(8分)
∴S阴影=S扇形GOB-S△OHB=![]() -
-![]() ×6×6
×6×6![]() =24
=24![]()
![]() .(10分)
.(10分)


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com