Question

小红学完“等腰三角形”和“勾股定理”后，进行了如下的探究：

等腰△ABC中，AB=AC，当AB²+AC²=BC²时，可得∠A=90°，即△ABC是等腰直角三角形（如图1）猜想：

【1】当AB²+AC²>BC²时，可得∠A<90°，即△ABC是等腰锐角三角形（如图2）；

【2】当AB²+AC²<BC²时，可得________，即___________________( 如图3)

　

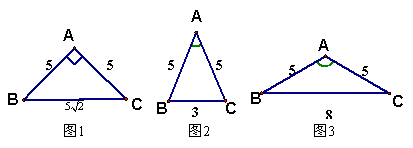
小红总结出：可以从等腰三角形三边的数量关系，进一步明确三角形的形状.

应用：（1）在图2的条件下（即AB=AC=5，BC=3），在边BC上是否存在点M，使MA与三角形的一腰垂直？ 请选择_______ A. 存在　　 B.不存在

　 （2）在图3的条件下（即AB=AC=5，BC=8），在边BC上是否存在点M，使得MA与三角形的一边垂直，若存在，请你求出满足条件时BM的长度；若不存在，请说明理由.

Answer 1

（1）猜想：当AB²+AC²<BC²时，可得∠A>90°，即△ABC是等腰钝角三角形（一空1分,共2分）

（2）应用：①___B__ ………………2分

②  [1] MA⊥AC , BM=   

[2] MA⊥BC , BM=  4

[3] MA⊥AB,BM=

评分标准：一个2分