
分析 根据分式的除法和加法进行化简即可,然后将x的值代入化简后的式子即可求得问题的答案.
解答 解:原式=$\frac{{x}^{2}}{(x+1)(x-1)}÷\frac{x-1+1}{x-1}$
=$\frac{{x}^{2}}{(x+1)(x-1)}×\frac{x-1}{x}$
=$\frac{x}{x+1}$.
∵x=2sin45°-1=2×$\frac{\sqrt{2}}{2}-1$=$\sqrt{2}-1$,
∴原式=$\frac{x}{x+1}=\frac{\sqrt{2}-1}{\sqrt{2}-1+1}=\frac{\sqrt{2}-1}{\sqrt{2}}$=$\frac{2-\sqrt{2}}{2}$.
点评 本题考查分式的化简求值、特殊三角函数的值,解题的关键是仔细认真进行计算,明确分式的加减乘除的法则,知道特殊三角函数的值.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
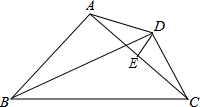 如图,点E为AC的中点,点D为△ABC外一点,且满足射线BD为∠ABC的平分线,∠ABC+∠ADC=180°,请判断DE和AC的位置关系,并证明.
如图,点E为AC的中点,点D为△ABC外一点,且满足射线BD为∠ABC的平分线,∠ABC+∠ADC=180°,请判断DE和AC的位置关系,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
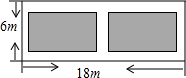 如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )| A. | (18-2x)(6-2x)=60 | B. | (18-3x)(6-x)=60 | C. | (18-2x)(6-x)=60 | D. | (18-3x)(6-2x)=60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com