
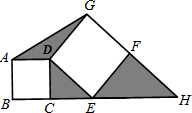
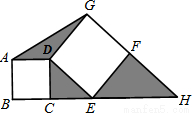
 如图,C是线段BE上一点,四边形ABCD是正方形,四边形DEFG也是正方形,BE和GF的延长线相交于点H,连接AG,若正方形ABCD的面积16,正方形DEFG的面积为36,则图中三个阴影三角形的面积之和等于________.
如图,C是线段BE上一点,四边形ABCD是正方形,四边形DEFG也是正方形,BE和GF的延长线相交于点H,连接AG,若正方形ABCD的面积16,正方形DEFG的面积为36,则图中三个阴影三角形的面积之和等于________.
 ,易证Rt△DEC≌Rt△DGM,得到GM=CE;易证得Rt△DCE∽Rt△DFH,则CE:FH=DC:EF,即2
,易证Rt△DEC≌Rt△DGM,得到GM=CE;易证得Rt△DCE∽Rt△DFH,则CE:FH=DC:EF,即2 :FH=4:6,求得FH=3
:FH=4:6,求得FH=3 ,于是有S三个阴影三角形的面积=
,于是有S三个阴影三角形的面积= AD•GM+
AD•GM+ DC•CE+
DC•CE+ EF•FH,代值计算即可.
EF•FH,代值计算即可.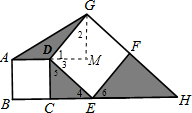
 =2
=2 ,
, :FH=4:6,
:FH=4:6, ,
, AD•GM+
AD•GM+ DC•CE+
DC•CE+ EF•FH
EF•FH ×4×2
×4×2 ×2+
×2+ ×6×3
×6×3
 .
. .
.

科目:初中数学 来源: 题型:
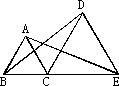
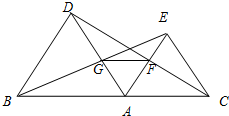 25、如图,A是线段CB上的一点,△ABD,△ACE都是等边三角形,AD与BE相交于点G,AE与CD相交于点F.
25、如图,A是线段CB上的一点,△ABD,△ACE都是等边三角形,AD与BE相交于点G,AE与CD相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:
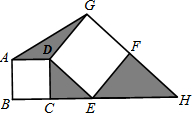 (2012•永嘉县一模)如图,C是线段BE上一点,四边形ABCD是正方形,四边形DEFG也是正方形,BE和GF的延长线相交于点H,连接AG,若正方形ABCD的面积16,正方形DEFG的面积为36,则图中三个阴影三角形的面积之和等于
(2012•永嘉县一模)如图,C是线段BE上一点,四边形ABCD是正方形,四边形DEFG也是正方形,BE和GF的延长线相交于点H,连接AG,若正方形ABCD的面积16,正方形DEFG的面积为36,则图中三个阴影三角形的面积之和等于| 5 |
| 5 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 沪科八年级版 2009-2010学年 第12期 总168期 沪科版 题型:044
如图,C是线段BE上一点,AC=BC=AB,CE=CD=DE,且△ACE和△BCD全等.请找出△ACE和△BCD中的对应边和对应角.
查看答案和解析>>
科目:初中数学 来源:2012年浙江省温州市永嘉县中考数学一模试卷(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com