解:(1)①BG=2BP.理由如下:
∵△ABC为等边三角形,
∴∠B=60°,
又∵GP⊥AB,
∴∠BPG=90°,
∴∠BGP=30°,
∴BG=2BP.
②∵AD⊥BC,
∴BD=

BC=

×2=1,
又∵BG=2BP=2x,
∴DG=BG-BD=2x-1(

<x≤1);
(2)∵PF∥AC,
∴△BPF为等边三角形,
∴BF=BP=x,
∴FD=1-x,
在Rt△EDG中,∠EGD=30°,DG=2x-1,
∴ED=

DG=

(2x-1),
∴S=

FD•ED=

•

(2x-1)(1-x)
=-

x
2+

x-

(

<x≤1),
当S=
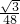
,则-

x
2+

x-

=
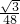
,
解得x
1=x
2=

∴x=

;
(3)∠EPF=∠EGD=30°,∠EDG=90°
当△PEF∽△GDE,
∴∠PEF=90°,
∴∠PFE=60°,
∴∠EFG=60°,
∴EF=2FD=2(1-x),
又∵PF=2EF,
∴x=4(1-x),解得x=

;
当△PFE∽△GDE,
∴∠PFE=90°,
∴∠EFD=30°,
∴EF=2DE=2×

FD=

(1-x),
而PF=

EF,
∴x=

•

(1-x),解得x=

,
∴以P、E、F为顶点的三角形与△EDG能相似,此时BP的长为

或

.
分析:(1)①由△ABC为等边三角形得到∠B=60°,而GP⊥AB,然后根据含30°的直角三角形三边的关系即可得到BG=2BP;②由AD⊥BC,根据等边三角形的性质得BD=

BC=

×2=1,即可得到DG=BG-BD=2x-1(

<x≤1);
(2)由PF∥AC易得△BPF为等边三角形,则BF=BP=x,得到FD=1-x,在Rt△EDG中根据含30°的直角三角形三边的关系得到ED=

DG=

(2x-1),然后利用三角形的面积公式即可得到S;当S=
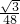
,得到关于x的一元二次方程,解方程即可;
(3)由∠EPF=∠EGD=30°,∠EDG=90°,再讨论:当△PEF∽△GDE,则∠PFE=90°;当△PFE∽△GDE,则∠PFE=90°,然后根据含30°的直角三角形三边的关系分别得到关于x的方程,解方程即可.
点评:本题考查了相似三角形的判定与性质:平行于三角形的一边的直线与其它两边(或其延长线)所截得的三角形与圆三角形相似.也考查了等边三角形的性质以及含30°的直角三角形三边的关系以及一元二次方程的解法.

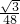 时x的值;
时x的值;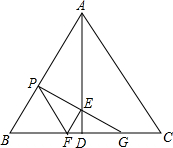 果不能,请说明理由.
果不能,请说明理由. BC=
BC= ×2=1,
×2=1, <x≤1);
<x≤1); DG=
DG= (2x-1),
(2x-1), FD•ED=
FD•ED= •
• (2x-1)(1-x)
(2x-1)(1-x) x2+
x2+ x-
x- (
( <x≤1),
<x≤1),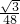 ,则-
,则- x2+
x2+ x-
x- =
=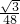 ,
,
 ;
; ;
; FD=
FD= (1-x),
(1-x), EF,
EF, •
• (1-x),解得x=
(1-x),解得x= ,
, 或
或 .
. BC=
BC= ×2=1,即可得到DG=BG-BD=2x-1(
×2=1,即可得到DG=BG-BD=2x-1( <x≤1);
<x≤1); DG=
DG= (2x-1),然后利用三角形的面积公式即可得到S;当S=
(2x-1),然后利用三角形的面积公式即可得到S;当S=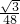 ,得到关于x的一元二次方程,解方程即可;
,得到关于x的一元二次方程,解方程即可;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的
如图,在边长为1的等边三角形ABC中,若将两条含120°圆心角的

 如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( )
如图,在边长为20cm的等边三角形ABC纸片中,以顶点C为圆心,以此三角形的高为半径画弧分别交AC、BC于点D、E,则扇形CDE所围的圆锥(不计接缝)的底圆半径为( ) 交AD于点E,交线段CD于点G,设BP=x.
交AD于点E,交线段CD于点G,设BP=x. (2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.
(2013•武汉模拟)如图,在边长为1的等边△OAB中,以边AB为直径作⊙D,以O为圆心OA长为半径作圆O,C为半圆AB上不与A、B重合的一动点,射线AC交⊙O于点E,BC=a,AC=b.