
���� ��1�����ݡ��ȶԽ��ı��Ρ��Ķ��壬���ı���ABCD�ǡ��ȶԽ��ı��Ρ�ʱ���ɷ���������������ۣ�������A=��C����B�١�D�����C=70�㣬�������ı����ڽǺͶ��������D��������B=��D����A�١�C�����D=80�㣬�������ı����ڽǺͶ��������C��
��2������ֱ��������б���ϵ����ߵ���б�ߵ�һ��ó�AD=DB=DC���ɵȱ߶ԵȽǵó���DCB=��B�����ɡ�B+��ACD=��DCB+��ACD=90�㣬��CED+��ACD=90�㣬����ͬ�ǵ������ȵó���CED=��B���֡�ECB�١�EDB�����ݡ��ȶԽ��ı��Ρ��Ķ��壬����֤���ı���BCED�ǡ��ȶԽ��ı��Ρ���
��3�����ݡ��ȶԽ��ı��Ρ��Ķ��壬���ı���CBDEΪ���ȶԽ��ı��Ρ�ʱ���ɷ���������������ۣ�������B=��DEC����BCE�١�BDE������AAS֤����CDE�ա�CDB������ȫ�������ζ�Ӧ����ȵó�EC=BC=3����ôAE=AC-EC=1��������BCE=��BDE=90�㣬��B�١�DEC�������ù��ɶ������AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5���ٸ��ݽ�ƽ���߶����ó�$\frac{AD}{BD}$=$\frac{AC}{BC}$=$\frac{4}{3}$�����AD=$\frac{4}{7}$AB=$\frac{20}{7}$����֤����ADE�ס�ACB������ͼ4����E��AC���ӳ����ϣ���CDB=��E����DCE�١�DBE��
����BE����C��CH��AB��H��DF��AC��F���Ƴ���DFC�ǵ���ֱ�������Σ��õ�DF=CF��ͨ����ADF�ס�ABC���õ�$\frac{AF}{AC}=\frac{DF}{BC}$�����DF=$\frac{12}{7}$���ٸ������������Ƶõ�$\frac{CE}{DH}$=$\frac{BC}{CH}$���õ�CE=$\frac{3}{7}$���ܵ�E��AC���ӳ����ϣ���ͼ5����CDB�١�E����DCE=��DBE������BE����E��EH��AB��AB���ӳ�����H���Ƴ���BHE�ǵ���ֱ�������Σ��������������ε����ʵõ�$\frac{AC}{AH}$=$\frac{BC}{EH}$���õ�BH=15�����ݹ��ɶ����õ�CE=$\sqrt{B{E}^{2}-B{C}^{2}}$=21�����ɵõ����ۣ�
��� ��1���⣺�ٵ���A�١�Cʱ�����ı���ABCD�ǡ��ȶԽ��ı��Ρ���
���D=��B=80�㣬
���C=360��-��A-��B-��D=360��-70��-80��-80��=130�㣬
�ڵ���A=��C=70��ʱ����D=360��-��A-��B-��C=360��-70��-80��-70��=140�㣬
���ϣ���C=70�㣬��D=140�㣬���C=130�㣬��D=80�㣻
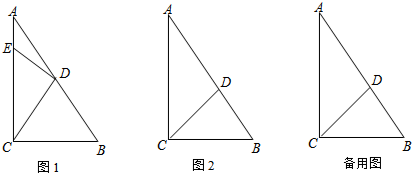
��2��֤������ͼ1����Rt��ABC�У�
��CDΪб��AB���ϵ����ߣ�
��AD=DB=DC��
���DCB=��B��
�ߡ�ACB=90�㣬
���DCB+��ACD=90�㣬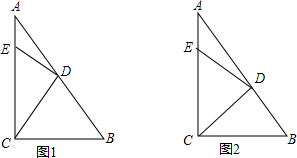 ���B+��ACD=90�㣮
���B+��ACD=90�㣮
��DE��CD��
���CED+��ACD=90�㣬
���CED=��B��
�ҡ�ECB�١�EDB��
���ı���BCED�ǡ��ȶԽ��ı��Ρ���
��3���⣺������B=��DEC����BCE�١�BDE����ͼ2��
�ڡ�CDE���CDB�У�
$\left\{\begin{array}{l}{��DEC=��B}\\{��DCE=��DCB}\\{CD=CD}\end{array}\right.$��
���CDE�ա�CDB��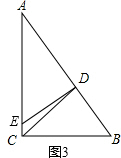 ��EC=BC=3��
��EC=BC=3��
��AE=AC-EC=4-3=1��
������BCE=��BDE=90�㣬��B�١�DEC����ͼ3��
����Rt��ACB�У���C=90�㣬AC=4��BC=3��
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5��
��CDƽ�֡�ACB��
��$\frac{AD}{BD}$=$\frac{AC}{BC}$=$\frac{4}{3}$��
��AD=$\frac{4}{7}$AB=$\frac{20}{7}$��
�ڡ�ADE���ACB�У�
$\left\{\begin{array}{l}{��A=��A}\\{��ADE=��ACB=90��}\end{array}\right.$��
���ADE�ס�ACB��
��$\frac{AE}{AB}$=$\frac{AD}{AC}$����$\frac{AE}{5}$=$\frac{\frac{20}{7}}{4}$��
��AE=$\frac{25}{7}$��
����ͼ4����E��AC���ӳ����ϣ���CDB=��E����DCE�١�DBE��
����BE����C��CH��AB��H��DF��AC��F��
��DF��BC��
��CDƽ�֡�ACB��
���DFC�ǵ���ֱ�������Σ�
��DF=CF��
��DF��BC��
���ADF�ס�ABC��
��$\frac{AF}{AC}=\frac{DF}{BC}$����$\frac{4-DF}{4}=\frac{DF}{3}$��
��DF=$\frac{12}{7}$��
��CD=$\frac{12\sqrt{2}}{7}$��
��CH=$\frac{AC•BC}{AB}$=$\frac{12}{5}$��
��DH=$\sqrt{C{D}^{2}-C{H}^{2}}$=$\frac{12}{35}$��
�ߡ�CHD=��BCE=90�㣬��CDH=��E��
���CDH�ס�BCE��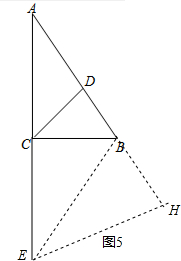
��$\frac{CE}{DH}$=$\frac{BC}{CH}$��
��CE=$\frac{3}{7}$��
��AE=AC+CE=$\frac{31}{7}$��
�ܵ�E��AC���ӳ����ϣ���ͼ5����CDB�١�E����DCE=��DBE��
����BE����E��EH��AB��AB���ӳ�����H��
��CDƽ�֡�ABC��
���DCE=��DBE=135�㣬
���EBH=45�㣬
���BHE�ǵ���ֱ�������Σ�
��BH=HE��
�ߡ�A=��A����ACB=��H=90�㣬
���ABC�ס�AEH��
��$\frac{AC}{AH}$=$\frac{BC}{EH}$����$\frac{4}{5+BH}$=$\frac{3}{BH}$��
��BH=15��
��BE=15$\sqrt{2}$��
��CE=$\sqrt{B{E}^{2}-B{C}^{2}}$=21��
��AE=AC+CE=25��
���������߶�AE�ij�Ϊ1��$\frac{25}{7}$��$\frac{31}{7}$��25��
���� �������ı����ۺ��⣬��Ҫ�������ı����ڽǺͶ�����ֱ�������Ρ����������ε����ʣ�ȫ�������Ρ����������ε��ж������ʣ���ǵ����ʣ����ɶ��������⡰�ȶԽ��ı��Ρ��Ķ��岢�����÷�������˼���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.25��10-5 | B�� | 25��10-7 | C�� | 2.5��10-6 | D�� | 2.5��10-5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
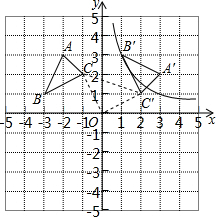 ��ABC�Ķ�������ΪA��-2��3����B��-3��1����C��-1��2����������ԭ��OΪ��ת���ģ�˳ʱ����ת90�㣬�õ���A��B��C�䣬��B�䡢C��ֱ��ǵ�B��C�Ķ�Ӧ�㣮
��ABC�Ķ�������ΪA��-2��3����B��-3��1����C��-1��2����������ԭ��OΪ��ת���ģ�˳ʱ����ת90�㣬�õ���A��B��C�䣬��B�䡢C��ֱ��ǵ�B��C�Ķ�Ӧ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
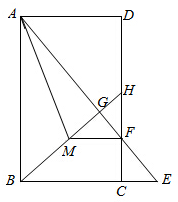 ��ͼ��ʾ���ھ���ABCD�У���E�DZ�BC�ӳ�����һ�㣬����AE����DC�ڵ�F����BH��AE�ڵ�G����DC�ڵ�H����FM��BC��BH�ڵ�M������AM����FH=FE��AD=2$\sqrt{7}$��AG=6��
��ͼ��ʾ���ھ���ABCD�У���E�DZ�BC�ӳ�����һ�㣬����AE����DC�ڵ�F����BH��AE�ڵ�G����DC�ڵ�H����FM��BC��BH�ڵ�M������AM����FH=FE��AD=2$\sqrt{7}$��AG=6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
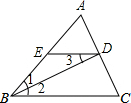 ��ͼ����ABC�У�BA=BC��BD�������εĽ�ƽ���ߣ�DE��BC��AB��E�����н��ۣ��١�1=��3����DE=$\frac{1}{2}$AB����S��ADE=$\frac{1}{4}$S��ABC����ȷ���У�������
��ͼ����ABC�У�BA=BC��BD�������εĽ�ƽ���ߣ�DE��BC��AB��E�����н��ۣ��١�1=��3����DE=$\frac{1}{2}$AB����S��ADE=$\frac{1}{4}$S��ABC����ȷ���У�������| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻ��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����ס����������50ǧ��ʱ��ʱ��t��ֵ����У�������
�ס���������A�dz���������ʻ��B�ǣ���������ʻ�����У��ס��������뿪A�ǵľ���y��ǧ�ף���׳���ʻ��ʱ��t��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����ס����������50ǧ��ʱ��ʱ��t��ֵ����У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪�����ϵĵ�A��B��C��D�ֱ��ʾ��-2��1��2��3�����ʾ��5-$\sqrt{5}$�ĵ�PӦ�����߶Σ�������
��ͼ����֪�����ϵĵ�A��B��C��D�ֱ��ʾ��-2��1��2��3�����ʾ��5-$\sqrt{5}$�ĵ�PӦ�����߶Σ�������| A�� | AO�� | B�� | OB�� | C�� | BC�� | D�� | CD�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com