
分析 由前4个数得出第n个数为(-1)n+1•$\frac{n}{(2n)^{2}-1}$,据此可得.
解答 解:∵第1个数$\frac{1}{3}$=(-1)2×$\frac{1}{{2}^{2}-1}$,
第2个数-$\frac{2}{15}$=(-1)3×$\frac{2}{{4}^{2}-1}$,
第3个数$\frac{3}{35}$=(-1)4×$\frac{3}{{6}^{2}-1}$,
第4个数-$\frac{4}{63}$=(-1)5×$\frac{4}{{8}^{2}-1}$,
…
∴第5个数为(-1)6×$\frac{5}{1{0}^{2}-1}$=$\frac{5}{99}$,
第6个数为(-1)7×$\frac{6}{1{2}^{2}-1}$=-$\frac{6}{143}$,
故答案为:$\frac{5}{99}$、-$\frac{6}{143}$.
点评 本题主要考查数字的变化规律,根据已知数列得出第n个数为(-1)n+1•$\frac{n}{(2n)^{2}-1}$是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 单项式乘以单项式,其结果一定仍是单项式 | |
| B. | 两个单项式相乘,积的系数是这两个单项式系数的积 | |
| C. | 两个单项式相乘,积的次数是这两个单项式次数的积 | |
| D. | 两个单项式相乘,每一个因式所含字母都在结果里出现 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
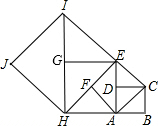 如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )
如图,如果以正方形ABCD的对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去…,已知正方形ABCD的面积S1为1,按上述方法所作的正方形的面积依次为S2,S3,…,Sn(n为正整数),那么第Sn个正方形的面积( )| A. | 2n | B. | 2n | C. | 2n-1 | D. | 2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2与-$\frac{1}{2}$ | B. | |-2|与$\frac{1}{2}$ | C. | |-2|与-2 | D. | -|-2|与-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com