
已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点.
(1)如图,若∠AOB=60°,求抛物线C的解析式;
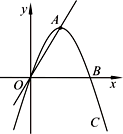
(2)如图,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线![]() ,求抛物线C、
,求抛物线C、![]() 的解析式;
的解析式;

(3)在(2)的条件下,设![]() 为抛物线
为抛物线![]() 的顶点,求抛物线C或
的顶点,求抛物线C或![]() 上使得PB=P
上使得PB=P![]() 的点P的坐标.
的点P的坐标.
|
(1)连接AB.∵A点是抛物线C的顶点,且C交x轴于O、B,∴AO=AB, 又∵∠AOB=60°,∴△ABO是等边三角形 1分 过A作AD⊥x轴于D,在Rt△OAD中,易求出OD=2,AD= ∴顶点A的坐标为(2, 设抛物线C的解析式为 ∴抛物线C的解析式为 (2)过A作AE⊥OB于E, ∵抛物线C: 又∵直线OA的解析式为y=x,∴AE=OE=2,∴点A的坐标为(2,2) 4分 将A、B、O的坐标代入 ∴抛物线C的解析式为 又∵抛物线C、 (3)作 由前可知,抛物线 作MH⊥x轴于H,易证△MHN∽△BHM,则 ∴ ∵直线l过点M(1,-1)、N( 解 ∴在抛物线C上存在两点使得 P1( 解 ∴在抛物线 P3(-5+ (用两点间的距离公式解决亦可) |


科目:初中数学 来源: 题型:044
如图,已知抛物线P:y=ax2+bx+c(a≠0) 与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:
|
x |
… |
-3 |
-2 |
1 |
2 |
… |
|
y |
… |
- |
-4 |
- |
0 |
… |
(1)
求A、B、C三点的坐标;(2)
若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;(3)
当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年浙江省金华、丽水市高级中等学校招生考试数学 题型:044
如图,已知抛物线![]() 与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
与直线y=2x交于点O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
查看答案和解析>>
科目:初中数学 来源:2007中考夺标冲刺模拟题(新课标)(二)、数学 题型:044
如图,已知抛物线![]() 与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.
与直线y=x交于A、B两点,与y轴交于点C,OA=OB,BC∥x轴.

(1)求抛物线的解析式.
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方),DE=![]() ,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
,过D、E两点分别作y轴的平行线,交抛物线于F、G,若设D点的横坐标为x,四边形DEGF的面积为y,求x与y之间的关系式,写出自变量x的取值范围,并回答x为何值时,y有最大值.
查看答案和解析>>
科目:初中数学 来源:湖北省十堰市2006年课改实验区初中毕业生学业考试数学 题型:044
已知抛物线C1:y=-x2+2mx+n(m,n为常数,且m≠0,n>0)的顶点为A,与y轴交于点C;抛物线C2与抛物线C1关于y轴对称,其顶点为B,连接AC,BC,AB.
注:抛物线y=ax2+bx+c(a≠0)的顶点坐标为![]() .
.
(1)请在横线上直接写出抛物线C2的解析式:________;
(2)当m=1时,判定△ABC的形状,并说明理由;
(3)抛物线C1上是否存在点P,使得四边形ABCP为菱形?如果存在,请求出m的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2007年资阳市初中毕业升学统一考试、数学试卷 题型:059
如图,已知抛物线P:y=ax2+bx+c(a≠0)与x轴交于A、B两点(点A在x轴的正半轴上),与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F、G分别在线段BC、AC上,抛物线P上部分点的横坐标对应的纵坐标如下:


(1)求A、B、C三点的坐标;
(2)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系,并指出m的取值范围;
(3)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=k·DF,若点M不在抛物线P上,求k的取值范围.
若因为时间不够等方面的原因,经过探索、思考仍无法圆满解答本题,请不要轻易放弃,试试将上述(2)、(3)小题换为下列问题解答(已知条件及第(1)小题与上相同,完全正确解答只能得到5分):
(2)若点D的坐标为(1,0),求矩形DEFG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com