
【题目】(本题10分)如图,已知二次函数![]() 的图象的顶点为A,二次函数
的图象的顶点为A,二次函数![]() 的图象与
的图象与![]() 轴交于原点O及另一点C,它的顶点B在函数
轴交于原点O及另一点C,它的顶点B在函数![]() 的图象的对称轴上.
的图象的对称轴上.
(1) 求点A与点C的坐标;
(2) 当四边形AOBC为菱形时,求函数![]() 的关系式.
的关系式.

【答案】(1)A的坐标为(1,﹣2),C的坐标为(2,0).
(2)二次函数y=ax2+bx的关系式为y=﹣2x2+4x.
【解析】试题分析:(1)二次函数y=ax2+bx的顶点在已知二次函数抛物线的对称轴上,可知两个函数对称轴相等,因此先根据已知函数求出对称轴.根据函数解析式得出顶点A的坐标与对称轴,故可得出二次函数y=ax2+bx关于x=1对称,且函数与x轴的交点分别是原点和C点,所以点C和点O关于直线l对称,故可得出点C的坐标;
(2)因为四边形AOBC是菱形,根据菱形性质,可以得出点O和点C关于直线AB对称,点B和点A关于直线OC对称,因此,可求出点B的坐标,根据二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),将B,C代入解析式得出ab的值,进而得出其解析式.
试题解析:(1)∵y=x2-2x-1=(x-1)2-2,
∴顶点A的坐标为(1,-2).
∵二次函数y=ax2+bx的图象与x轴交于原点O及另一点C,它的顶点B在函数y=x2-2x-1的图象的对称轴上.
∴二次函数y=ax2+bx的对称轴为:直线x=1,
∴点C和点O关于直线x=1对称,
∴点C的坐标为(2,0).
(2)因为四边形AOBC是菱形,所以点B和点A关于直线OC对称,
因此,点B的坐标为(1,2).
因为二次函数y=ax2+bx的图象经过点B(1,2),C(2,0),
所以![]()
解得![]() ,
,
所以二次函数y=ax2+bx的关系式为y=-2x2+4x.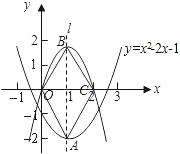


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】(本题10分)我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形,不妨简称为“锅线”,锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图①所示(图②是备用图),如果把锅纵断面的抛物线记为C1,把锅盖纵断面的抛物线记为C2.
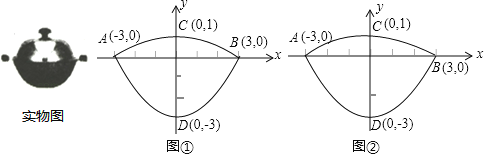
(1)求C1和C2的解析式;
(2)如果炒菜时锅的水位高度是1dm,求此时水面的直径;
(3)如果将一个底面直径为3dm,高度为3dm的圆柱形器皿放入炒菜锅内蒸食物,锅盖能否正常盖上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式组![]() 无解,则a的取值范围是__.
无解,则a的取值范围是__.
【答案】a≥7
【解析】![]()
解①得
![]() ;
;
解②得
![]() ;
;
∵不等式组无解,
∴a≥7.
点睛:本题考查了一元一次不等式组的知识,解一元一次不等式组的应用,解此题的关键是能根据不等式组无解得出关于m的不等式组.
【题型】填空题
【结束】
21
【题目】解不等式组:![]() ,并把它的解集在数轴上表示出来.
,并把它的解集在数轴上表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?(每天的总成本=每件的成本×每天的销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com