
 的图象相交于点A(﹣1,2)、点B(﹣4,n)
的图象相交于点A(﹣1,2)、点B(﹣4,n)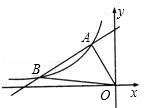
 x+
x+ (2)
(2)
 =
= .
. 中,2=
中,2=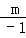 ;
; .(2分)
.(2分) 中,n=﹣
中,n=﹣ ;
; .
. ).(3分)
).(3分) )的坐标分别代入y=kx+b中,
)的坐标分别代入y=kx+b中,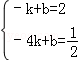 ,解得
,解得 .
. x+
x+ ;
; x+
x+ =0,x=﹣5;
=0,x=﹣5;
 •OC•|yA|=
•OC•|yA|= ×5×2=5.
×5×2=5. •OC•|yB|=
•OC•|yB|= ×5×
×5× =
= .
. =
= .
. 中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.
中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.

 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源:不详 题型:解答题
 ,OB=4,OE=2.
,OB=4,OE=2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象相交于A,B两点,已知A(1,4).
的图象相交于A,B两点,已知A(1,4).
 的解集.
的解集.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .
相交于点A(1,b)、点B(c,﹣2),求k+a的值.甲同学说:未知数太多,很难求的;乙同学说:可能不是用待定系数法来求;丙说:如果用数形结合的方法,利用两交点在坐标系中位置的特殊性,可以试试.请结合他们的讨论求出k+a= .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 (x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y=
(x>0)的图象分别交于点A1、A2、A3、A4、…;与函数y= 的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1,四边形A2A3B3B2的面积记为S2,四边形A3A4B4B3的面积记为S3,…,以此类推.则S10的值是( )
的图象分别交于点B1、B2、B3、B4、….如果四边形A1A2B2B1的面积记为S1,四边形A2A3B3B2的面积记为S2,四边形A3A4B4B3的面积记为S3,…,以此类推.则S10的值是( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com