
分析 (1)n边形的内角和是(n-2)•180°,少计算了一个内角,结果得2750°.则内角和是(n-2)•180°与2750°的差一定小于180度,并且大于0度.因而可以解方程(n-2)•180°≥2750°,多边形的边数n一定是最小的整数值,从而求出多边形的边数;
(2)先求出多边形的内角和,再减去2750°,即可求出少加的那个内角度数.
解答 解:(1)设多边形的边数是n.
依题意有(n-2)•180°≥2750°,
解得:n≥17$\frac{5}{18}$,
则多边形的边数n=18;
(2)多边形的内角和是(18-2)•180°=2880°;
则少加的那个内角的大小为2880°-2750°=130°.
点评 本题考查了多边形内角与外角,正确理解多边形内角的大小的特点,以及多边形的内角和定理是解决本题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:填空题
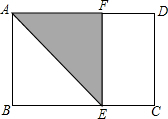 将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$.
将长为1,宽为a的矩形纸片ABCD($\frac{1}{2}$<a<1)按如图方式折叠,剪下一个边长等于矩形宽度的正方形ABEF.若剩下的矩形EFDC与矩形ABCD相似,则a=$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
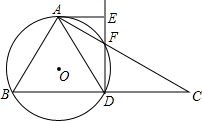 如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.
如图,在Rt△ABC中,斜边BC=12,∠C=30°,D为BC的中点,△ABD的外接圆⊙O与AC交于F点,过A作⊙O的切线AE交DF的延长线于E点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )
如图,在水池的正中央有一根芦苇,池底长10尺,它高出水而1尺,如果把这根芦苇拉向水池一边,它的顶端恰好到达池边的水面则这根芦苇的长度是( )| A. | 10尺 | B. | 11尺 | C. | 12尺 | D. | 13尺 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF,则下列结论中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com