
分析 (1)根据“凤凰”方程得:a+b+c=0①,根据有两个相等的实数根得△=0②,①②式结合得:a=c;
(2)先将原方程化简为一般形式,再将x=1代入得:n=3-2m;计算△=9,所以方程有两个不相等实根,且是整数,根据求根公式求出x的值,利用已知条件求出整数m的值.
解答 解:(1)由题意得:a+b+c=0,b=-a-c,
∵ax2+bx+c=0(a≠0)有两个相等的实数根,
∴△=b2-4ac=0,
把b=-a-c代入到b2-4ac=0中得:(-a-c)2-4ac=0,
(a-c)2=0,
∴a=c;
(2)m(x2+1)-3x2+nx=0,
(m-3)x2+nx+m=0,
当x=1时,2m-3+n=0,n=3-2m,
△=n2-4m(m-3)=n2-4m2+12m=(3-2m)2-4m2+12m=9,
∴x=$\frac{-n±\sqrt{9}}{2(m-3)}$=$\frac{-n±3}{2m-6}$=$\frac{2m-3±3}{2m-6}$,
x1=$\frac{m}{m-3}$,x2=1,
因为方程两个实数根都是整数,
∴整数m为0或2或4或6.
点评 本题考查了根与系数的关系和根的判别式,也属于新概念问题;给出一个新概念-“凤凰”方程,根据“凤凰”方程解决相应问题;熟练掌握一元二次方程的求根公式,并熟知一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.上面的结论反过来也成立.


科目:初中数学 来源: 题型:选择题
| A. | -(-1.2)和-1.2 | B. | +(-1.2)和-(-1.2) | C. | -(-1.2)和|-1.2| | D. | -(-1.2)和-|-1.2| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
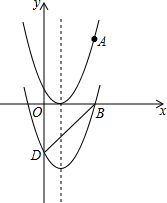 如图,抛物线C1:y=a(x-1)2经过点A(3,4).
如图,抛物线C1:y=a(x-1)2经过点A(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
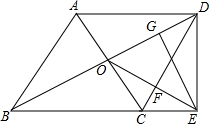 如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.
如图,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,EG⊥BD,垂足为为G,连接DE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com