练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．若将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（　　）
    A．（-1，0）B．（-1，-1）C．（-2，0）D．（-2，-1）

    分析 根据横坐标，右移加，左移减；纵坐标，上移加，下移减可得点B的坐标为（1-2，3-4），进而可得答案．

    解答 解：将点A（1，3）向左平移2个单位，再向下平移4个单位得到点B，则点B的坐标为（1-2，3-4），
    即（-1，-1），
    故选：B．

    点评 此题主要考查了坐标与图形的变化--平移，关键是掌握点的坐标的变化规律．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

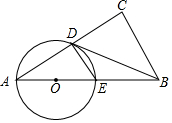    5．如图，在Rt△ABC中，∠C=90°，点D是AC的中点，过点A、D作⊙O，⊙O与AB交于点E，AE是⊙O的直径，AD是⊙O的一条弦，且∠A+∠CDB=90°，AD：AE=4：5，BC=6．
    （1）求证：直线BD与⊙O相切；
    （2）下面是根据题中条件求直径AE长的过程，阅读后请按要求解决下列问题：
    解法1．∵AE是⊙O的直径，∴∠ADE=90°=∠C，∴DE∥BC
    又∵D是AC的中点，∴$\frac{AE}{AB}$=$\frac{DE}{BC}$=$\frac{1}{2}$=$\frac{AD}{AC}$，∴E是AB的中点，∴DE=$\frac{1}{2}$BC=3．
    在Rt△ADE中，设AD=4x，AE=5x，∴（4x）2+32=（5x）2，
    解之得：x1=1，x2=-1（舍去），∴AE=5x=5，即⊙O的直径为5．
    解法2．∵∠A+∠CDB=90°，又∵∠A+∠CBA=90°，∴∠CDB=∠CBA，∠C=∠C，
    ∴△DCB∽△BCA，∴$\frac{DC}{BC}$=$\frac{BC}{AC}$，∴BC2=DC•AC，又∵AC=2DC=2AD，∴BC2=AD•2AD，
    AD=$\frac{4}{5}$AE，62=2×（$\frac{4}{5}$AE）2，AE=$\frac{15}{4}$$\sqrt{2}$．
    以上两种解法结果不同，那么问题出在哪里呢？
    ①下列说法正确的是D
    A．解法1有错     B．解法2有错     C．解法1、2都有错    
    D．解法1、2都没错，但题中条件“AD：AE=4：5”是多余的
    ②在①中若你选择的是A、B、C中一个，请说明错在哪里？若你选的是D，请删去“AD；AE=4：5”这个条件，求出⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．把下列各式因式分解
    （1）ap-aq+am
    （2）a2-4
    （3）a2-2a+1
    （4）ax2+2axy+ay2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．有四根细木棒，长度分别为 3cm、5cm、7cm、9cm，以其中任意三条为边可以构成3个三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．代数式$\frac{\sqrt{1-x}}{x+2}$有意义，则字母x的取值范围是x≤1且x≠-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

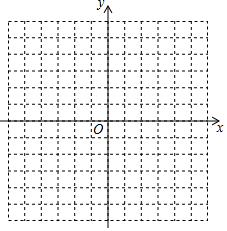    20．（1）在如图所示的平面直角坐标系中表示下面各点：
    A（0，3）；B（5，0）；C（3，-5）；D（-3，-5）；E（3，5）；
    （2）A点到原点的距离是3．
    （3）将点C向x轴的负方向平移6个单位，它与点D重合．
    （4）连接CE，则直线CE与y轴是什么位置关系？
    （5）点D分别到x、y轴的距离是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．解不等式：$\frac{3x+20}{2}$-1＞6x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（　　）
    A．$\left\{\begin{array}{l}x+y=100\\ 3x+3y=100\end{array}\right.$B．$\left\{\begin{array}{l}x+y=100\\ x+\frac{1}{3}y=100\end{array}\right.$
    C．$\left\{\begin{array}{l}x+y=100\\ 3x+\frac{1}{3}y=100\end{array}\right.$D．$\left\{\begin{array}{l}x+y=100\\ 3x+y=100\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

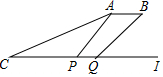    5．某日，正在我国南海海域作业的一艘大型渔船突然发生险情，相关部门接到求救信号后，立即调遣一架直升飞机和一艘刚在南海巡航的渔政船前往救援，伤员在C处，直升机在A处，伤员离云梯（AP）150米（即CP的长）．伤员从C地前往云梯的同时，直升机受到惯性的影响又往前水平行进50米到达B处，此时云梯也移动到BQ位置，已知∠ACP=30°，∠APQ=60°，∠BQI=43°．问：伤员需前行多少米才能够到云梯？（结果保留整数，sin43°=0.68，cos43°=0.73，tan43°=0.93，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    同步练习册答案