
从甲地到乙地,先是一段平路,然后是一段上坡路。小明骑车从甲地出发,到达乙地后立即原路返回甲地,途中休息了一段时间。假设小明骑车在平路、上坡、下坡时分别保持匀速前进.已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km。设小明出发xh后,到达离甲地y km的地方,图中的折线OABCDE表示y与x之间的函数关系.
(1)小明骑车在平路上的速度为 km/h;他途中休息了 h;
(2)求线段AB,BC所表示的y与 之间的函数关系式;
之间的函数关系式;
(3)如果小明两次经过途中某一地点的时间间隔为0.15h,那么该地点离甲地多远?
(1)15,0.1;(2)y=10x+1.5(0.3≤x≤0.5),y=-20x+16.5(0.5<x≤0.6);(3)5.5km
解析试题分析:(1)由速度=路程÷时间就可以求出小明在平路上的速度,就可以求出返回的时间,进而得出途中休息的时间.
(2)先由函数图象求出小明到达乙地的时间就可以求出B的坐标和C的坐标就可以由待定系数法求出解析式.
(3)小明两次经过途中某一地点的时间间隔为0.15h,由题意可以得出这个地点只能在破路上.设小明第一次经过该地点的时间为t,则第二次经过该地点的时间为(t+0.15)h,根据距离甲地的距离相等建立方程求出其解即可.
试题解析:(1)∵小明骑车在平路上的速度为:4.5÷0.3=15,
∴小明骑车在上坡路的速度为:15-5=10,小明骑车在下坡路的速度为:15+5=20.
∴小明返回的时间为:(6.5-4.5)÷20+0.3=0.4小时.
∴小明骑车到达乙地的时间为:0.3+2÷10=0.5小时.
∴小明途中休息的时间为:1-0.5-0.4=0.1小时.
(2)∵小明骑车到达乙地的时间为0.5小时,∴B(0.5,6.5).
∵小明下坡行驶的时间为:2÷20=0.1,∴C(0.6,4.5).
设直线AB的解析式为y=k1x+b1,由题意,得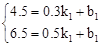 ,解得:
,解得: .
.
∴线段AB所表示的y与x之间的函数关系式为y=10x+1.5(0.3≤x≤0.5).
设直线BC的解析式为y=k2+b2,由题意,得 ,解得:
,解得: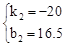 .
.
∴线段BC所表示的y与x之间的函数关系式y=-20x+16.5(0.5<x≤0.6).
(3)小明两次经过途中某一地点的时间间隔为0.15h,由题意可以得出这个地点只能在破路上.
设小明第一次经过该地点的时间为t,则第二次经过该地点的时间为(t+0.15)h,
由题意,得10t+1.5=-20(t+0.15)+16.5,解得:t=0.4.
∴y=10×0.4+1.5=5..
∴该地点离甲地5.5km.
考点:1.一次函数的应用;2.直线上点的坐标与方程的关系;3.待定系数法的应用;4.方程思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
小明家距离学校8千米,今天早晨小明骑车上学途中,自行车突然“爆胎”,恰好路边有便民服务点,几分钟后车修好了,他加快速度骑车到校,我们根据小明的这段经历画了一幅图象,该图描绘了小明行驶路程s与所用时间t之间的函数关系,请根据图象回答下列问题:
(1)小明骑车行驶了多少千米时,自行车“爆胎”修车用了几分钟?
(2)小明共用多长时间到学校的?
(3)小明修车前的速度和修车后的速度分别是多少?
(4)如果自行车未“爆胎”,小明一直按修车前速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:直线y=x+1经过点B(2,n),且与x轴交于点A.
(1)求n及点A坐标.
(2) 若点P是x轴上一点,且△APB的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在平面直角坐标系中,等腰Rt△AOB的斜边OB在x轴上,直线 经过等腰Rt△AOB的直角顶点A,交y轴于C点.
经过等腰Rt△AOB的直角顶点A,交y轴于C点.
(1) 求点A坐标;
(2)若点P为x轴上一动点.点Q的坐标是( ,
, ),△PAQ是以点A为直角顶点的等腰三角形.求出
),△PAQ是以点A为直角顶点的等腰三角形.求出 的值并写出点Q的坐标.
的值并写出点Q的坐标.
(3)在(2)的条件下,若D是坐标平面内任意一点,使点A、P、Q、D刚好能构成平行四边形,请直接写出符合条件的点D的坐标
.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
做服装生意的王老板经营甲、乙两个店铺,每个店铺在同一段时间内都能售出A、B两种款式的服装合计30件,并且每售出一件A款式和B款式服装,甲店铺获利润分别为30元和35元,乙店铺获利润分别为26元和36元.某日,王老板进A款式服装36件,B款式服装24件,并将这批服装分配给两个店铺各30件.
(1)怎样将这60件服装分配给两个店铺,能使两个店铺在销售完这批服装后所获利润相同?
(2)怎样分配这60件服装能保证在甲店铺获利润不小于950元的前提下,王老板获利的总利润最大?最大的总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一天,某渔船离开港口前往黄岩岛海域捕鱼,8小时后返航,此时一艘渔政船从该港口出发前往黄岩岛巡查(假设渔政船与渔船沿同一航线航行)。下图是渔政船及渔船到港口的距离S和渔船离开港口的时间t之间的函数图象.
(1)写出渔船离港口的距离S和它离开港口的时间t的函数关系式;
(2)在渔船返航途中,什么时间范围内两船间距离不超过30海里?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=- x+b,求n的值.
x+b,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,直线 与x轴相交于点A,与直线
与x轴相交于点A,与直线 相交于点P(2,
相交于点P(2, ).
).
(1)请判断 的形状并说明理由.
的形状并说明理由.
(2)动点E从原点O出发,以每秒1个单位的速度沿着O→P→A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥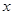 轴于F,EB⊥
轴于F,EB⊥ 轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
轴于B.设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:① S与t之间的函数关系式.
② 当t为何值时,S最大,并求S的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com