练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA，探究∠DBC与∠ABC度数的比值，请你完成下列探究过程：
    先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明。
    （1）当∠BAC= 90°时，依问题中的条件补全下图，观察图形，AB与AC的数量关系为____；
    当推出∠DAC=15°时，可进一步推出∠DBC的度数为____；
    可得到∠DBC与∠ABC度数的比值为：____；
    （2）当∠BAC≠90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明。
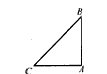
    解：（1）如图（1），相等15°；1/3；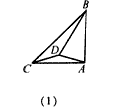
    （2）猜想：∠DBC与∠ABC度数的比值与（1）中结论相同，
    证明：如图（2），作∠KCA= ∠BAC，
    过B点作BK//AC交CK于点K，连接DK，
    ∵∠BAC≠90°，
    ∴四边形ABKC是等腰梯形，
    ∴CK=AB，
    ∵DC=DA，
     ∴∠DCA=∠DAC，
    ∵∠KCA=∠BAC，
    ∴∠KCD=∠3，
    ∴△KCD≌△BAD，
    ∴∠2=∠4，KD= BD，
    ∴KD=BD=BA=KC，
    ∵BK//AC，
    ∴∠ACB=∠6，
    ∵∠KCA=2∠ACB，
    ∴∠5=∠ACB，
    ∴∠5=∠6，
    ∴KC=KB，
    ∴KD=BD=KB，
    ∴∠KBD=60°，
    ∵∠ACB=∠6=60°- ∠l，
    ∴∠BAC=2∠ACB=120°-2∠1，
    ∵∠l+（60°-∠l）+（120°-2∠1）+∠2 =180°，
    ∴∠2=2∠1，
    ∴∠DBC与∠ABC度数的比值为1/3。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：阅读理解

    25、阅读下面问题的解决过程：
    问题：已知△ABC中，P为BC边上一定点，过点P作一直线，使其等分△ABC的面积．
    解决：
    情形1：如图①，若点P恰为BC的中点，作直线AP即可．
    情形2：如图②，若点P不是BC的中点，则取BC的中点D，连接AP，
    过点D作DE∥AP交AC于E，作直线PE，直线PE即为所求直线．
    问题解决：
    如图③，已知四边形ABCD，过点B作一直线（不必写作法），使其等分四边形ABCD的面积，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

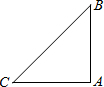    20、问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA．探究∠DBC与∠ABC度数的比值．
    请你完成下列探究过程：
    先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
    （1）当∠BAC=90°时，依问题中的条件补全右图；
    观察图形，AB与AC的数量关系为
    相等
    ；当推出∠DAC=15°时，可进一步推出∠DBC的度数为
    15°
    ；可得到∠DBC与∠ABC度数的比值为
    1：3
    ；
    （2）当∠BAC＜90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

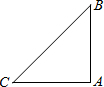    问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA．探究∠DBC与∠ABC度数的比值．
    请你完成下列探究过程：
    先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
    （1）当∠BAC=90°时，依问题中的条件补全右图；
    观察图形，AB与AC的数量关系为______；当推出∠DAC=15°时，可进一步推出∠DBC的度数为______；可得到∠DBC与∠ABC度数的比值为______；
    （2）当∠BAC＜90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明．

    查看答案和解析>>

    科目：初中数学 来源：2013年贵州省黔西南州中考数学模拟试卷（六）（解析版） 题型：解答题

    问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA．探究∠DBC与∠ABC度数的比值．
    请你完成下列探究过程：
    先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
    （1）当∠BAC=90°时，依问题中的条件补全右图；
    观察图形，AB与AC的数量关系为______；当推出∠DAC=15°时，可进一步推出∠DBC的度数为______；可得到∠DBC与∠ABC度数的比值为______；
    （2）当∠BAC＜90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明．

    查看答案和解析>>

    科目：初中数学 来源：2010年全国中考数学试题汇编《三角形》（16）（解析版） 题型：解答题

    （2010•北京）问题：已知△ABC中，∠BAC=2∠ACB，点D是△ABC内的一点，且AD=CD，BD=BA．探究∠DBC与∠ABC度数的比值．
    请你完成下列探究过程：
    先将图形特殊化，得出猜想，再对一般情况进行分析并加以证明．
    （1）当∠BAC=90°时，依问题中的条件补全右图；
    观察图形，AB与AC的数量关系为______；当推出∠DAC=15°时，可进一步推出∠DBC的度数为______；可得到∠DBC与∠ABC度数的比值为______；
    （2）当∠BAC＜90°时，请你画出图形，研究∠DBC与∠ABC度数的比值是否与（1）中的结论相同，写出你的猜想并加以证明．

    查看答案和解析>>

    同步练习册答案