Question

如图15.1，已知抛物线C经过原点，对称轴x=-3与抛物线相交于第三象限的点M，与x轴相交于点N，且tan∠MON = 3.

(1)求抛物线C的解析式；

(2)将抛物线C绕原点O旋转180º得到抛物线C’，抛物线C’与x轴的另一交点为A，B为抛物线C’上横向坐标为2的点.

①若P为线段AB上一动点，PD⊥y轴于点D，求△APD面积的最大值；

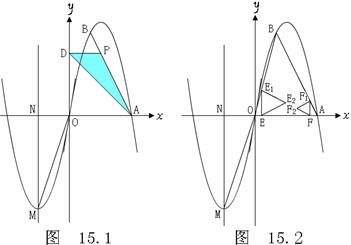②过线段OA上的两点E、F分别作x轴的垂线，交折线 O –B -A于点E₁、F₁，再分别以线段EE₁、FF₁为边作如图15.2所示的等边△EE₁E₂、等边△FF₁F₂,点E以每秒1个单位长度的速度从点O向点A运动，点F以每秒1个单位长度的速度从点A向点O运动，当△EE₁E₂有一边与△FF₁F₂的某一边在同一直线上时，求时间t的值.

Answer 1

解：（1）对称轴MN的解析式为x =-3, ON=3,tan∠MON = 3 ,MN=9,M（-3，-9），

令抛物线C的解析式为y=a(x+3)²-9，它经过原点，则0=a(0+3)²-9, a=1,

y=1(x+3)²-9=x²+6x ，所以抛物线C的解析式为y=x²+6x；

（2）①抛物线C’的解析式为

y=- x²+6x，当y=0时，x=0或6，点A的坐标为（6，0）， 点B在抛物线C’上，且其横坐标为2，y=8,有点B（2，8），直线AB的解析式为

y=-2x +12 ,点P在线段AB上，令点P的坐标为（p,-2p+12）,

S_△APD = p(-2p+12)=- p²+6p =-(p-3)²+9,当p=3（2<3<8）时，

S_△APD 的max值为9；

② 据（2）①知，直线OB解析式为y=4x,

直线AB解析式为y=-2x +12；

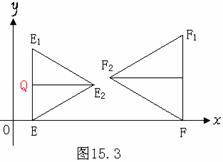
如图15.3, ∵EE₁//FF₁, △EE₁E₂、△FF₁F₂是等边三角形，∴E₁E₂//FF₂，EE₂//F₁F₂，

直线EE₁的解析式为x=t,直线FF₁的解析式为x=6-t,令E₁ (t,y)则有E（t,0）、

E₂ (t+ ,)，设直线EE₂的解析式为

y=x + a,直线F₁F₂的解析式为y= x + b,直线E₁E₂的解析式

为y=- x + c,直线FF₂的解析式为y=- x + d，

Ⅰ、当EE₁与FF₁在同一直线上时，x=t=6-t，t=3 ；

Ⅱ、当0≤t≤2时，点E₁在直线OB上，点F₁在直线AB上，有E（t,0）、E₁ (t,4t)、F (6-t,0)、F₁（6-t,2t）

(a)当EE₂与F₁F₂在同一直线上时，有0 = t + a，a=- t,

2t= (6-t) + b, b= (2+ )t-2, a=b, - t=(2+ )t-2,

t= ；

(b) 当E₁E₂与FF₂在同一直线上时，有4t=- t + c，c=(4+ )t,

0=- (6-t) + d, d=2- t, c=d, (4+ )t = 2 - t,

t= ；

通过作图观察可知，当2<t≤6时，EE₁与FF₁不可能在同一直线上，E₁E₂与FF₂也不可能在同一直线上。

综上所述，当△EE₁E₂有一边与△FF₁F₂的某一边在同一直线上时，t的值为3，或 .

下面的讨论旨在说明2< t≤6时，EE₁与FF₁、E₁E₂与FF₂的位置关系，答题时可以省去。

[ Ⅲ、当2 <t≤4时，点E₁在直线AB上，点F₁在直线AB上，有E（t,0）、E₁ (t,-2t+12)、F (6-t,0)、F₁（6-t,2t）

(a)当EE₂与F₁F₂在同一直线上时，有0 = t + a，a=- t,

2t= (6-t) + b, b= (2+ )t-2, a=b, - t=(2+ )t-2,

t= （< 2，舍去）；

(b) 当E₁E₂与FF₂在同一直线上时，有-2t+12=- t + c，c=(-2)t+12,

0=- (6-t) + d, d=2- t, c=d, (-2)t+12 = 2 - t,

t= (>4,舍去)；

 Ⅳ、当4<t≤6时，点E₁在直线AB上，点F₁在直线OB上，有E（t,0）、E₁ (t,-2t+12)、F (6-t,0)、F₁（6-t,24-4t），

(a)当EE₂与F₁F₂在同一直线上时，有0= t + a, a=- t,

 24-4t= (6-t) + b, b=24-2+ t-4t,a=b,

- t=24-2+ t-4t, t= (>6,舍去)；

(b) 当E₁E₂与FF₂在同一直线上时，有-2t+12=- t + c, c=12+ t-2t, 0=- (6-t) + d , d=2- t , c = d,

12+ t-2t=2- t ,t= (>6,舍去)；

综上所述，当△EE₁E₂有一边与△FF₁F₂的某一边在同一直线上时，

t的值为3，或 .  ]