
如图,一次函数y=kx+b与反比例函数y= 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.

1.求一次函数与反比例函数的解析式;
2.根据所给条件,请直接写出不等式kx+b> 的解集
的解集
3.过点B作BC⊥x轴,垂足为C,求S△ABC
1.y=x+1;
y=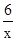
2.-3<x<0或x>2
3.5
【解析】解:(1)∵点A(2,3)在y=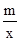 的图象上,
的图象上,
∴m=6,……………………………………………………………… 1分
∴反比例函数的解析式为y=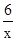 ………………………………………2分
………………………………………2分
∴n=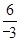 =-2,
=-2,
∵点A(2,3),B(-3,-2)在y=kx+b的图象上,
∴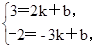
∴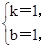
∴一次函数的解析式为y=x+1.……………………………………4分
(2)-3<x<0或x>2;…………………………………………6分
(3)方法一:设AB交x轴于点D,则D的坐标为(-1,0),
∴CD=2,……………………………………………………………7分
∴S△ABC=S△BCD+S△ACD
=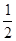 ×2×2+
×2×2+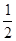 ×2×3=5.
×2×3=5.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,一次函数y1=ax+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C,与x轴交于点D.

(1)求a、k的值;
(2)过点A作AE⊥x轴于点E,若P为反比例函数图象的位于第一象限部分上的一点,且直线OP分△ADE所得的两部分面积之比为2∶7.请求出所有符合条件的点P的坐标;
(3)在(2)的条件下,请在x轴上找一点Q,使得△PQC的周长最小,并求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
(11·柳州)(本题满分6分).
如图,一次函数y=-4x-4的图象与x轴、y轴分别交于A、C

(1)求抛物线的函数表达式;
(2)设抛物线的顶点为D,求四边形ABDC的面积;
(3)作直线MN平行于x轴,分别交线段AC、BC于点M、N.问在x轴上是否存在点P,使得△PMN是等腰直角三角形?如果存在,求出所有满足条件的P点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2012届湖北省随州市四校中考模拟联考数学卷(带解析) 题型:填空题
如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数y= 的图象相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连结CF、DE,有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④△DCE≌△CDF,其中正确的结论是______(把你认为正确结论的序号填上。)
的图象相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连结CF、DE,有下列四个结论:①△CEF与△DEF的面积相等;②△AOB∽△FOE;③AC=BD;④△DCE≌△CDF,其中正确的结论是______(把你认为正确结论的序号填上。)
查看答案和解析>>
科目:初中数学 来源:2013届浙江省兰溪市梅江初中九年级上学期期中考试数学试卷(带解析) 题型:解答题
(本题6分)如图,一次函数y=ax+b的图像与反比例函数 的图像交于M、N两点。
的图像交于M、N两点。
求:(1)反比例函数与一次函数的解析式。
(2)根据图像写出反比例函数的值不小于一次函数的值的x的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com