�⣺��1������A
1��1��0��S
1=
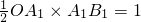
��A
1B
1=2
����B
1��1��2��
����˫����Ϊ��
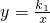
������B
1��1��2���ã�k
1=2
��
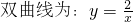
�ڡ�A
2������2��0��
��B
2������Ϊ2������˫���߽���ʽ��B
2��������2��1��
��ֱ��A
1B
2����ʽΪ��y=k
2x+b
����A
1��1��0����B
2��2��1����
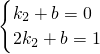
��ã�
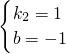
��ֱ��A
1B
2��Ӧ�ĺ�������ʽΪy=x-1��
��2������A
n������n��0����B
n����Ϊn
��B
n���������˫���߽���ʽ�е�
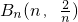
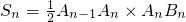
=
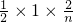
=

��
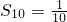
��3��OB
1ֱ�߷���Ϊy=2x
��

��
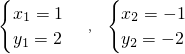
��
��P����������-1��-2��
��A
n-1��n-1��0����B
n��n��

���ɵ�ֱ��A
n-1B
n��Ӧ�ĺ�������ʽΪ��
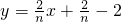
����
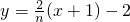
����㣨-1��-2����
��ֱ��A
1B
2��A
2B
3��A
n-1B
n��������P��-1��-2����
��������1����Ҫ��˫���߽���ʽ��ֻ�����˫�����ϵ�һ���������꼴�ɣ������⣬�ɴ�B�����֣�
��2���ڵ�n���������У�A
n��������n��0����B
n������Ϊn�����루1������õĽ���ʽ�ɵó�B
n�����꣬�Ӷ����AB
n��Rt��A
n-1A
nB
n�����ʽ
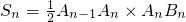
�����n�������ε��������ʽ���ٴ���n��ֵ���������Ҫ��õ������ε������
��3�����P�����꣬�ٽ��ֱ��A
n-1B
n��ͨʽ������P���������㣮
���������⿼����˫������ֱ�ߵ����ã���ֱ����˫���߽���ʽ����������������꣮����ʱ�ҳ��������ͨʽѰ�Һ����Ľ��ⷽ�����ǽ������Ĺؼ���

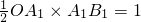
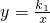 ������B1��1��2���ã�k1=2
������B1��1��2���ã�k1=2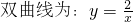
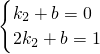 ��ã�
��ã�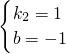
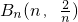
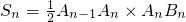 =
=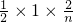 =
=
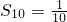
 ��
��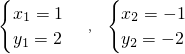 ��
�� ���ɵ�ֱ��An-1Bn��Ӧ�ĺ�������ʽΪ��
���ɵ�ֱ��An-1Bn��Ӧ�ĺ�������ʽΪ��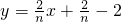
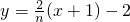
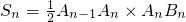 �����n�������ε��������ʽ���ٴ���n��ֵ���������Ҫ��õ������ε������
�����n�������ε��������ʽ���ٴ���n��ֵ���������Ҫ��õ������ε������

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
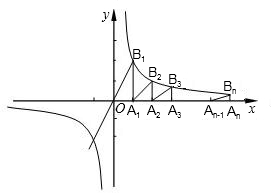
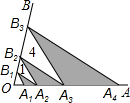 ��ͼ����A1��A2��A3��A4������OA�ϣ���B1��B2��B3������OB�ϣ���A1B1��A2B2��A3B3��A2B1��A3B2��A4B3������A2B1B2����A3B2B3������ֱ�Ϊ1��4����ͼ��������Ӱ���������֮��Ϊ
��ͼ����A1��A2��A3��A4������OA�ϣ���B1��B2��B3������OB�ϣ���A1B1��A2B2��A3B3��A2B1��A3B2��A4B3������A2B1B2����A3B2B3������ֱ�Ϊ1��4����ͼ��������Ӱ���������֮��Ϊ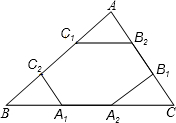 ��ͼ����A1��A2��B1��B2��C1��C2�ֱ��ǡ�ABC�ı�BC��CA��AB�����ȷֵ㣬����ABC���ܳ�ΪL����������A1A2B1B2C1C2���ܳ�Ϊ��������
��ͼ����A1��A2��B1��B2��C1��C2�ֱ��ǡ�ABC�ı�BC��CA��AB�����ȷֵ㣬����ABC���ܳ�ΪL����������A1A2B1B2C1C2���ܳ�Ϊ��������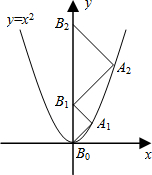 ��ͼ����A1��A2��A3������An��������y=x2ͼ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn-1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2012B2011B2012������=
��ͼ����A1��A2��A3������An��������y=x2ͼ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn-1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2012B2011B2012������= ��ͼ����A1��A2��A3������An��������y=x2ͼ���ϣ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn-1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2013B2012B2013������=
��ͼ����A1��A2��A3������An��������y=x2ͼ���ϣ���B1��B2��B3������Bn��y���ϣ�����A1B0B1����A2B1B2��������AnBn-1Bn��Ϊ����ֱ�������Σ���B0������ԭ�㣩�����A2013B2012B2013������=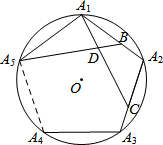 ��2013•�Ͼ���ģ����ͼ����A1��A2��A3��A4��A5�ڡ�O�ϣ���
��2013•�Ͼ���ģ����ͼ����A1��A2��A3��A4��A5�ڡ�O�ϣ���



