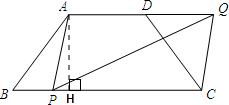
解:(1)作AH⊥BC于点H.
∵cosB=

,AB=5,
∴BH=3,AH=4.
在Rt△AHP中,
AP=
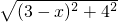
=
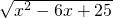
.
(2)∵
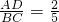
,
∴
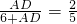
.
∴AD=4,BC=10.
∵AD∥BC,
∴∠PAQ=∠APB.
∵∠APQ=∠B.
∴△APQ∽△PBA.
∴
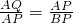
.
∴
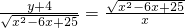
.
∴y=
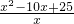
.
定义域为0<x≤10;
(3)要使△CPQ与△ABP相似,必须有∠PQC=∠B或∠PCQ=∠B.
(i)如果∠PQC=∠B,那么∠APQ=∠PQC.
∴AP∥CQ.
∵AQ∥PC,
∴四边形APCQ是平行四边形.
∴AQ=PC,即y+4=10-x.
∴
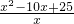
+4=10-x.
整理,得2x
2-16x+25=0.
∴x=
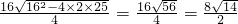
.
(ⅱ)如果∠PCQ=∠B时,那么点Q与点D重合.
∴y=0,即
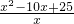
=0.
∴x=5.
综上所述,△CPQ与△ABP能相似,此时BP=
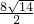
或5.
分析:(1)过A作AH⊥BC于点H,可以求出AH,BH的长度,然后在Rt△AHP中,利用勾股定理表示AP的长度;
(2)先利用
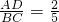
与等腰梯形的性质求出AD、BC的长度,然后证明△APQ和△PBA相似,根据相似三角形对应边成比例的性质列出比例式,再代入数据进行整理即可得到y关于x的函数解析式;
(3)要使△CPQ与△ABP相似,因为可以证明∠BAP=∠CPQ,所以还必须有∠PQC=∠B或∠PCQ=∠B,因此需要分两种情况进行讨论,根据相似三角形对应边成比例列比例式进行求解即可.
点评:本题主要考查了等腰梯形的性质,相似三角形的判定与性质,勾股定理,以及解直角三角形,综合性较强,需要结合图形,对各知识点综合考虑并灵活运用方能解决.

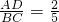 ,
,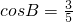 ,P是边BC上的一个动点,
,P是边BC上的一个动点,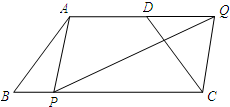 ∠APQ=∠B,PQ交射线AD于点Q.设点P到点B的距离为x,点Q到点D的距离为y.
∠APQ=∠B,PQ交射线AD于点Q.设点P到点B的距离为x,点Q到点D的距离为y. 解:(1)作AH⊥BC于点H.
解:(1)作AH⊥BC于点H. ,AB=5,
,AB=5,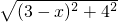 =
=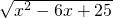 .
.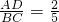 ,
,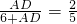 .
.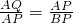 .
.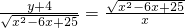 .
.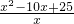 .
.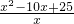 +4=10-x.
+4=10-x.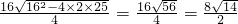 .
.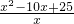 =0.
=0.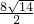 或5.
或5.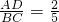 与等腰梯形的性质求出AD、BC的长度,然后证明△APQ和△PBA相似,根据相似三角形对应边成比例的性质列出比例式,再代入数据进行整理即可得到y关于x的函数解析式;
与等腰梯形的性质求出AD、BC的长度,然后证明△APQ和△PBA相似,根据相似三角形对应边成比例的性质列出比例式,再代入数据进行整理即可得到y关于x的函数解析式;

 阅读快车系列答案
阅读快车系列答案 9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G.
9、如图,已知在梯形ABCD中,AD∥BC,AB=DC,对角线AC和BD相交于点O,E是BC边上一个动点(E点不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点G. 如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.
如图,已知在梯形ABCD中,AD∥BC,点E在边BC上,连接DE,AC.