
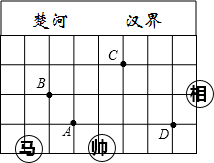
 中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图①中“马”所在的位置可以直接走到点A或点B处.
中国象棋棋盘中蕴含着平面直角坐标系,如图是中国象棋棋盘的一半,棋子“马”走的规则是沿“日”形的对角线走.例如:图①中“马”所在的位置可以直接走到点A或点B处.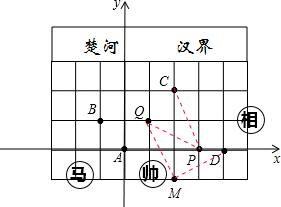 解:(1)建立如图所示的平面直角坐标系:点A为坐标原点.
解:(1)建立如图所示的平面直角坐标系:点A为坐标原点.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
| A、1.6×10-7m |
| B、1.6×10-6m |
| C、1.6×10-5m |
| D、16×10-6m |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
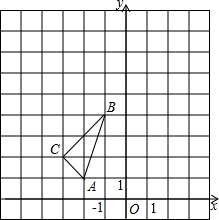 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).查看答案和解析>>
科目:初中数学 来源: 题型:
|
查看答案和解析>>
科目:初中数学 来源: 题型:
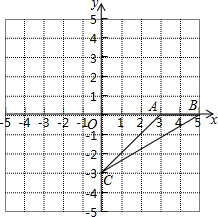 在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.
在平面直角坐标系中,△ABC的顶点坐标是A(3,0),B(5,0),C(0,-3).点P(m,n)为△ABC内一点,平移△ABC到△A1B1C1,使点P(m,n)移到点P1(m-4,n+2)处.查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| 4 |
| 5 |
| 3 |
| 2 |
| 5 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.
某中学八年级共有400名学生,学校为了增强学生的环保意识,在本年级进行了一次环保知识测验.为了了解这次测验的成绩状况,学校从中抽取了50名学生的成绩,将所得数据整理后,画出的频数分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com