
【题目】如图,在梯形ABCD中,AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点,连接AF、FG,过点D作DE∥FG交AF于点E. 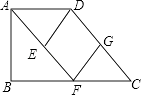
(1)求证:△AED≌△CGF;
(2)若梯形ABCD为直角梯形,∠B=90°,判断四边形DEFG是什么特殊四边形?并证明你的结论;
(3)若梯形ABCD的面积为a(平方单位),则四边形DEFG的面积为(平方单位).(只写结果,不必说理)
【答案】
(1)证明:∵BC=2AD,点F为BC的中点,
∴CF=AD.
又∵AD∥BC,
∴四边形AFCD是平行四边形,
∴∠DAE=∠C,AF∥DC,
∴∠AFG=∠CGF.
∵DE∥GF,
∴∠AED=∠AFG,
∴∠AED=∠CGF
∴△AED≌△CGF;
(2)解:结论:四边形DEFG是菱形.
证明如下:连接DF.
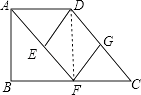
由(1)得AF∥DC,
又∵DE∥GF,
∴四边形DEFG是平行四边形.
∵AD∥BC,AD=BF= ![]() BC,
BC,
∴四边形ABFD是平行四边形,
又∵∠B=90°,
∴四边形ABFD是矩形,
∴∠DFC=90°,
∵点G是CD的中点,
∴FG=DG= ![]() CD,
CD,
∴四边形DEFG是菱形;
(3)![]() a
a
【解析】(3)四边形DEFG的面积=梯形ABCD的面积﹣S△ABF﹣2S△CFG ,
∵梯形ABCD的面积为a,
∴四边形DEFG的面积为 ![]() a;
a;
【考点精析】根据题目的已知条件,利用梯形的定义的相关知识可以得到问题的答案,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线C的解析式为y=ax2+bx+c,则下列说法中错误的是( )
A.a确定抛物线的形状与开口方向
B.若将抛物线C沿y轴平移,则a,b的值不变
C.若将抛物线C沿x轴平移,则a的值不变
D.若将抛物线C沿直线l:y=x+2平移,则a、b、c的值全变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%.甲、乙两种商品原来的单价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中小方格边长为1,请你根据所学的知识解决下面问题.
(1)求网格图中△ABC的面积.
(2)判断△ABC是什么形状?并所明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
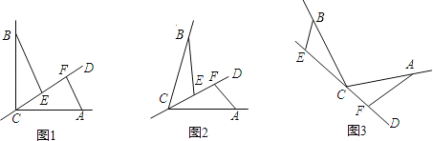
【题目】CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE_____CF;EF_____|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件_____,使①中的两个结论仍然成立。
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并给出理由。.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿EF折叠,使点B与CD的中点B′重合,若AB=2,BC=3,则△FCB′与△B′DG的面积之比为( )
A.9:4
B.3:2
C.16:9
D.4:3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com