
 如图,矩形OBAC的两边OC、OB在坐标轴上,另两边AB、AC分别与双曲线
如图,矩形OBAC的两边OC、OB在坐标轴上,另两边AB、AC分别与双曲线 (k>0)交于F、E两点,且A点坐标为(4,3),S△OEF=
(k>0)交于F、E两点,且A点坐标为(4,3),S△OEF= ,则k=________.
,则k=________. ,再由E与F都为反比例函数图象上的点,将设出的两点分别入反比例解析式中,得到a与n的关系式,用a表示出n,代入an=
,再由E与F都为反比例函数图象上的点,将设出的两点分别入反比例解析式中,得到a与n的关系式,用a表示出n,代入an= 中,求出n的值,即可确定出k的值.
中,求出n的值,即可确定出k的值. 解:过E作EM⊥x轴,交x轴于点M,如图所示,
解:过E作EM⊥x轴,交x轴于点M,如图所示, (k>0)上,
(k>0)上, ,n=
,n= ,即3a=4n=k,
,即3a=4n=k, OC•CE=
OC•CE= ×3a=
×3a= a,S△OBF=
a,S△OBF= OB•BF=
OB•BF= ×4n=2n,S矩形OCEM=3a=k,S梯形EFBM=
×4n=2n,S矩形OCEM=3a=k,S梯形EFBM= (3+n)(4-a),
(3+n)(4-a), ,
, ,即3a+
,即3a+ (3+n)(4-a)-
(3+n)(4-a)- a-2n=
a-2n= ,
, ,又3a=4n,即a=
,又3a=4n,即a= n,
n, n2=
n2= ,即n2=1,
,即n2=1,

科目:初中数学 来源: 题型:
 如图,矩形OBAC的两边OC、OB在坐标轴上,另两边AB、AC分别与双曲线y=
如图,矩形OBAC的两边OC、OB在坐标轴上,另两边AB、AC分别与双曲线y=| k |
| x |
| 16 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:2012年湖北省武汉市新洲区仓埠中学中考数学模拟试卷(3月份)(解析版) 题型:填空题
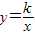 (k>0)交于F、E两点,且A点坐标为(4,3),S△OEF=
(k>0)交于F、E两点,且A点坐标为(4,3),S△OEF=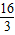 ,则k= .
,则k= .
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
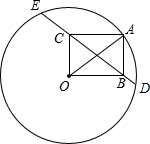 如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是________.
如图所示,点A在半径为20的圆O上,以OA为一条对角线作矩形OBAC,设直线BC交圆O于D、E两点,若OC=12,则线段CE、BD的长度差是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com