
【题目】已知函数f(x)=lnx+x2﹣2ax+1(a为常数).
(1)讨论函数f(x)的单调性;
(2)若对任意的 ![]() ,都存在x0∈(0,1]使得不等式
,都存在x0∈(0,1]使得不等式 ![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
【答案】
(1)解:由f(x)=lnx+x2﹣2ax+1,得 ![]() ,
,
令h(x)=2x2﹣2ax+1.
①当a≤0时,h(x)>0,则f'(x)>0成立,
△=4a2﹣8,当 ![]() 时,△≤0,则2x2﹣2ax+1≥0,h(x)≥0,即f'(x)≥0恒成立,
时,△≤0,则2x2﹣2ax+1≥0,h(x)≥0,即f'(x)≥0恒成立,
∴当 ![]() 时,f'(x)≥0,f(x)在(0,+∞)上单调递增;
时,f'(x)≥0,f(x)在(0,+∞)上单调递增;
②当 ![]() 时,由2x2﹣2ax+10≥0,得
时,由2x2﹣2ax+10≥0,得 ![]() 或
或 ![]() ,
,
由2x2﹣2ax+10<0,得 ![]() .
.
∴f(x)在 ![]() 上单调递增,在
上单调递增,在 ![]() 单调递减;
单调递减;
(2)解:∵ ![]() ,
,
∴f'(x)>0,f(x)在(0,1]单调递增,f(x)max=f(1)=2﹣2a,
存在x0∈(0,1]使得不等式 ![]() 成立,
成立,
即2﹣2a+lna>m(a﹣a2),
∵任意的 ![]() ,∴a﹣a2<0,即
,∴a﹣a2<0,即 ![]() 恒成立,
恒成立,
令 ![]() ,则
,则 ![]() ,
,
∵任意的 ![]() ,
, ![]() ,
,
∴ ![]() 是增函数,
是增函数,
∴ ![]() ,
,
∵ ![]() 恒成立,
恒成立,
∴实数m的取值范围 ![]() .
.
【解析】(1)求出原函数的导函数,当a≤0时,导函数恒大于0,然后利用二次函数的判别式对a分类讨论求出导函数在不同区间内的符号,得到原函数的单调性;(2)由(1)知, ![]() 时,函数f(x)在(0,1]上单调递增,求出函数在(0,1]上的最大值2﹣2a,把存在x0∈(0,1]使得不等式
时,函数f(x)在(0,1]上单调递增,求出函数在(0,1]上的最大值2﹣2a,把存在x0∈(0,1]使得不等式 ![]() 成立转化为2﹣2a+lna>m(a﹣a2),得到
成立转化为2﹣2a+lna>m(a﹣a2),得到 ![]() 恒成立,构造函数
恒成立,构造函数 ![]() ,求导可知为增函数,得其最大值,则实数m的取值范围可求.
,求导可知为增函数,得其最大值,则实数m的取值范围可求.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:初中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AD∥BC,AD=AB=DC= ![]() BC=1,E是PC的中点,面PAC⊥面ABCD.
BC=1,E是PC的中点,面PAC⊥面ABCD. 
(Ⅰ)证明:ED∥面PAB;
(Ⅱ)若PC=2,PA= ![]() ,求二面角A﹣PC﹣D的余弦值.
,求二面角A﹣PC﹣D的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为矩形,SD⊥底面ABCD,AD= ![]() ,DC=SD=2,点M在侧棱SC上,∠ABM=60°.
,DC=SD=2,点M在侧棱SC上,∠ABM=60°. 
(Ⅰ)证明:M是侧棱SC的中点;
(Ⅱ)求二面角S﹣AM﹣B的余弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知曲线C的极坐标方程为ρ﹣4cosθ+3ρsin2θ=0,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,直线l过点M(1,0),倾斜角为 ![]() . (Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
. (Ⅰ)求曲线C的直角坐标方程与直线l的参数方程;
(Ⅱ)若曲线C经过伸缩变换 ![]() 后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
后得到曲线C′,且直线l与曲线C′交于A,B两点,求|MA|+|MB|.
查看答案和解析>>
科目:初中数学 来源: 题型:
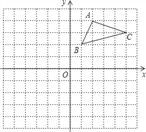
【题目】如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
(1)在直角坐标系中画出△ABC关于x轴的对称图形△A1B1C1;
(2)在直角坐标系中将△ABC向左平移4个单位长度得△A2B2C2,画出△A2B2C2;
(3)若点D(m,n)在△ABC的边AC上,请分别写出△A1B1C1和△A2B2C2 的对应点D1和D2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(﹣1,0)和F2(1,0),点M为BC边的中点.
(1)求点M的轨迹方程;
(2)设点M的轨迹为曲线T,直线MF1与曲线T另一个交点为N,线段MF2中点为E,记S=S ![]() +S
+S ![]() ,求S的最大值.
,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ① ![]() =
= ![]() ;②
;② ![]() =
= ![]() ;③
;③ ![]() ;④
;④ ![]() =
= ![]()
其中正确的个数有( )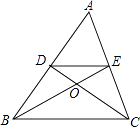
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com