
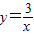 图象上的点P1(1,y1),P2(2,y2),…,Pn(n,Pn)….作x轴的垂线,垂足分别为A1,A2…An …,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,依此类推,则点Bn的纵坐标是 .(结果用含n代数式表示)
图象上的点P1(1,y1),P2(2,y2),…,Pn(n,Pn)….作x轴的垂线,垂足分别为A1,A2…An …,连接A1P2,A2P3,…,An-1Pn,…,再以A1P1,A1P2为一组邻边画一个平行四边形A1P1B1P2,以A2P2,A2P3为一组邻边画一个平行四边形A2P2B2P3,依此类推,则点Bn的纵坐标是 .(结果用含n代数式表示)
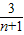 +
+ =
= .
. 的图象上,
的图象上, ;
; +3,即点B1的纵坐标是
+3,即点B1的纵坐标是 ;
; =
= ;
; +1=
+1= ;
; +
+ =
= ;
; .
.

科目:初中数学 来源: 题型:
 如图,一次函数的图象与反比例函数y1=-
如图,一次函数的图象与反比例函数y1=- | 3 |
| x |
| a |
| x |
| 3 |
| x |
| a |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
查看答案和解析>>
科目:初中数学 来源:2005年江苏省镇江中学高中单独招生考试数学试卷(解析版) 题型:解答题
 (k为非零常数)的图象上的一动点.
(k为非零常数)的图象上的一动点.
查看答案和解析>>
科目:初中数学 来源:江苏中考真题 题型:填空题
 点A在y轴的正半轴上,过点A作直线
点A在y轴的正半轴上,过点A作直线 ,AC:AB=2:3,则k1=( ),k2=( )。
,AC:AB=2:3,则k1=( ),k2=( )。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com