
【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;
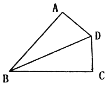
(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

【答案】(1)角平分线上的点到角的两边距离相等;(2)证明见解析;(3)证明见解析.
【解析】
(1)根据角平分线的性质定理解答;
(2)作DE⊥BA交BA延长线于E,DF⊥BC于F,证明△DEA≌△DFC,根据全等三角形的性质证明;
(3)在BC时截取BK=BD,连接DK,根据(2)的结论得到AD=DK,根据等腰三角形的判定定理得到KD=KC,结合图形证明.
(1)∵BD平分∠ABC,∠BAD=90°,∠BCD=90°,∴DA=DC(角平分线上的点到角的两边距离相等).
故答案为:角平分线上的点到角的两边距离相等;
(2)如图2,作DE⊥BA交BA延长线于E,DF⊥BC于F.
∵BD平分∠EBF,DE⊥BE,DF⊥BF,∴DE=DF.
∵∠BAD+∠C=180°,∠BAD+∠EAD=180°,∴∠EAD=∠C.
在△DEA和△DFC中,∵ ,∴△DEA≌△DFC(AAS),∴DA=DC;
,∴△DEA≌△DFC(AAS),∴DA=DC;
(3)如图,在BC时截取BK=BD,连接DK.
∵AB=AC,∠A=100°,∴∠ABC=∠C=40°.
∵BD平分∠ABC,∴∠DBK![]() ∠ABC=20°.
∠ABC=20°.
∵BD=BK,∴∠BKD=∠BDK=80°,即∠A+∠BKD=180°,由(2)的结论得AD=DK.
∵∠BKD=∠C+∠KDC,∴∠KDC=∠C=40°,∴DK=CK,∴AD=DK=CK,∴BD+AD=BK+CK=BC.




科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A按逆时针方向旋转,得到矩形AEFG,E点正好落在边CD上,连接BE,BG,且BG交AE于P.
(1)求证:∠CBE=![]() ∠BAE;
∠BAE;
(2)求证:PG=PB;
(3)若AB=![]() ,BC=3,求出BG的长.
,BC=3,求出BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点,分别过点
上一动点,分别过点![]() 作
作![]() ,
,![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() 的值;
的值;
(2)探究:当点![]() 满足什么条件时,
满足什么条件时,![]() 的值最小?最小值是多少?
的值最小?最小值是多少?
(3)根据(2)中的结论,请构造图形求代数式![]() 的最小值.
的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△EFC都是等腰直角三角形,∠ACB=∠ECF=90°,点E在AB边上.

(1)求证:△ACE≌△BCF;
(2)若∠BFE=60°,求∠AEC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com