【答案】
分析:根据一次函数的性质得到a>0,b<0,再根据二次函数的性质得到抛物线开口向上,抛物线的对称轴在y轴的右侧,抛物线过原点,由此可得到正确答案.
解答:解:∵y=ax+b的图象过第一、三、四象限,
∴a>0,b<0,
对于y=ax
2+bx的图象,
∵a>0,
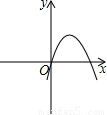
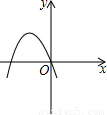
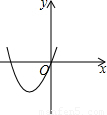
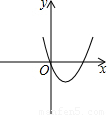
∴抛物线开口向上,
∵x=-

>0,
∴抛物线的对称轴在y轴的右侧,
∵c=0,
∴抛物线过原点.
故选D.
点评:本题考查了二次函数的图象与系数的关系:二次函数y=ax
2+bx+c(a≠0)的图象为抛物线,当a>0,抛物线开口向上;对称轴为直线x=-

;抛物线与y轴的交点坐标为(0,c).也考查了一次函数的性质.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案